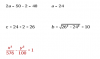-
en una clase de 50 alumnos cual es la probabilidad de coincida el cumpleaños con el del profesor?
ros
el 26/3/17 -
Hola, tengo el siguiente ejercicio de subespacios vectoriales. Lo he resuelto, el problema esque nose si es correcta la solución y si lo es, podrias explicarme el concepto del subespacio Columna y Fila porque no lo tengo muy claro.
Gracias.
Antonius Benedictus
el 26/3/17Jefferson
el 26/3/17 -
 Podriais ayudarme con el C, esta hecho, pero no entiendo de donde sale el senoalfa-senoalfacosenoalfa+senalfa+senalfacosenoalfa
Podriais ayudarme con el C, esta hecho, pero no entiendo de donde sale el senoalfa-senoalfacosenoalfa+senalfa+senalfacosenoalfaAntonio Silvio Palmitano
el 26/3/17Tienes la expresión trigonométrica:
sena/(1+cosa) + sena/(1-cosa) =
extraes mínimo común denominador (observa que es el producto de los denominadores):
= ( sena(1-cosa) + sena(1+cosa) ) / (1+cosa)(1-cosa) =
distribuyes en el numerador, y también en el denominador:
= (sena - sena*cosa + sena + sena*cosa) / (1 - cosa + cosa - cos2a) =
reduces términos semejantes en el numerador y también en el denominador (observa que tienes cancelaciones):
= 2*sena/(1 - cos2a) =
aplicas la identidad del cuadrado del seno en función del cuadrado del coseno en el denominador y queda:
= 2*sena/sen2a =
simplificas:
= 2/sena.
Espero haberte ayudado.
-
de cuantas maneras se pueden colocar 8 torres en el tablero de ajedrez sin que se amenacen?
Antonio Silvio Palmitano
el 26/3/17Comienza por considerar al tablero de ajedrez como una cuadrícula de ocho filas y 8 columnas, y observa que en cada fila debes colocar una sola torre, y que en cada columna debes colocar una sola torre. Te sugiero que tomes tu tablero de ajedrez, y que emplees ocho monedas para ir ubicándolas una a una).
Luego tienes que para colocar:
la primera torre tienes 64 posibles lugares, luego cancelas su fila y su columna (observa que comparten una casilla) y tienes para
la segunda torre 64 - 15 = 49 lugares luego cancelas su fila y su columna (15 lugares), pero observa que dos lugares son compartidos con las filas o columnas canceladas anteriormente, por lo que tienes para
la tercera torre 49 - 13 = 36 lugares, luego cancelas su fila y su columna (15 lugares), pero observa que cuatro lugares son compartidos con las filas o columnas canceladas anteriormente, por lo que tienes para
la cuarta torre 36 - 11 = 25 lugares, luego cancelas su fila y su columna (15 lugares), pero observa que seis lugares son compartidos con las filas o columnas canceladas anteriormente, por lo que tienes para
la quinta torre 25 - 9 = 16 lugares, luego cancelas su fila y su columna (15 lugares), pero observa que ocho lugares son compartidos con las filas o columnas canceladas anteriormente, por lo que tienes para
la sexta torre 16 - 7 = 9 lugares, luego cancelas su fila y su columna (15 lugares), pero observa que diez lugares son compartidos con las filas o columnas canceladas anteriormente, por lo que tienes para
la séptima torre 9 - 5 = 4 lugares, luego cancelas su fila y su columna (15 lugares), pero observa que doce lugares son compartidos con filas o columnas canceladas anteriormente, por lo que tienes para
la octava torre 4 - 3 = 1 lugar disponible.
Luego, por el principio de multiplicación tienes (observa que al ubicar una torre tienes x posibilidades, y que para cada una de ellas tienes y posibilidades para ubicar la siguiente) que para ubicar ocho torres sin que compartan fila o columna, tienes que la cantidad de posibilidades es:
N = 64*49*36*25*16*9*4*1 = 82*72*62*52*42*32*22*12 =
= (8*7*6*5*4*3*2*1)2 =
= (8!)2 =
= (40320)2 =
= 1625702400.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 26/3/17Recuerda que el tablero de ajedrez está formado por 32 cuadrados blancos y 32 cuadrados negros (es muy conveniente que recurras a tu tablero de ajedrez).
Tienes dos casos: a) eliges primero el cuadrado blanco, y b) eliges primero el cuadrado negro.
a)
Para elegir el cuadrado blanco tienes 32 posibilidades,
luego, cancelas la fila y la columna correspondiente y quedan 49 casillas, pero observa que has cancelado 15 cuadrados, 8 negros y 7 blancos (observa que la casilla que has elegido es compartida por su fila y su columna), por lo que tienes disponibles 24 cuadrados negros y 25 cuadrados blancos, por lo que
para elegir el cuadrado negro tienes 24 posibilidades,
y como por cada elección posible para el primer cuadrado tienes otra cantidad para elegir el segundo, por el principio de multiplicación tienes:
Na = 32*24 = 768 posibilidades.
b)
Para elegir el cuadrado negro tienes 32 posibilidades,
luego, cancelas la fila y la columna correspondiente y quedan 49 casillas, pero observa que has cancelado 15 cuadrados, 7 negros y 8 blancos (observa que la casilla que has elegido es compartida por su fila y su columna), por lo que tienes disponibles 25 cuadrados negros y 24 cuadrados blancos, por lo que
para elegir el cuadrado blanco tienes 24 posibilidades,
y como por cada elección posible para el primer cuadrado tienes otra cantidad para elegir el segundo, por el principio de multiplicación tienes:
Nb = 32*24 = 768 posibilidades.
Luego, por el principio de adición tenemos en total:
N = Na + Nb = 768 + 768 = 2*768 = 1536 posibilidades.
Espero haberte ayudado.
-
Vuelvo a poner la duda, con el ejercicio. El c.
"¿Podrías decirme cómo queda el límite al infinito? Creo que la segunda queda 38/0,4. Pero la función polinómica como queda?"

Ángel
el 26/3/17Antonio Silvio Palmitano
el 26/3/17Observa que el dominio de la función es D = R = (-∞,+∞), por lo que tenemos dos límites para plantear y resolver.
Para ello, operamos en las expresiones correspondientes:
a) En el primer trozo la expresión es:
x2 - 8x + 50 = extraemos factor común con el término principal = x2*(1 - 8/x + 50/x2),
luego pasamos al cálculo del límite:
Lím(x→-∞) (x2 - 8x + 50) = Lím(x→-∞) ( x2*(1 - 8/x + 50/x2) ) = +∞ (observa que el segundo factor tiende a 1).
b) En el segundo trozo la expresión es:
(38x - 100) / 0,4*x = extraemos factor común con el término principal en el numerador:
= x*(38 - 100/x) / 0,4*x = simplificamos = (38 - 100/x)/0,4,
luego pasamos al cálculo del límite:
Lím(x→+∞) (38x - 100) / 0,4*x = Lím(x→+∞) (38 - 100/x)/0,4 = (38 + 0)/0,4 = 38/0,4 = 95.
Espero haberte ayudado.
-
¡Hola! ¿Ayuda para resolver el ejercicio a y el c?
Maths, te pregunté en uno de los ejercicios que me ayudaste a resolver, ¿puedes mirarlo? gracias

Ángel
el 26/3/17¿En qué número de página del foro está la duda que dices? o manda un pantallazo para que vea a qué te refieres, pues acabo de echar un vistazo a las 7 primeras y me parece que no te he visto
Ah, y del ejercicio que acabas de mandar:
el apartado a) obviamente en x=3 es contínua, porque el trozo de x<4 (que incluye a x=3, claro) está regido por un función polinómica lineal (f(x)=x/2+5 en ese caso concreto...que por definición es contínua
el apartado c), la letra b tiene que valer 11 para ser contínua
-
Hola alguien me podría ayudar es muy urgente.
Determina la ecuación reducida de la hipérbola sabiendo que un foco dista de los vértices 2 y 50.
Antonio Silvio Palmitano
el 26/3/17Consideramos una Hipérbola con centro C(0,0) y eje focal OX (es muy aconsejable que hagas un dibujo).
Luego, observa que sus vértices tienen coordenadas (-a,0) y (a,0), con a > 0,
y observa que sus focos tienen coordenadas (-c,0) y (c,0), con c > 0.
Luego, tenemos para el foco cuyas coordenadas hemos remarcado, que sus distancias a cada uno de los vértices quedan planteadas:
c - (-a) = 50 (distancia entre el foco señalado y el vértice más lejano)
c - a = 2 (distancia entre el foco señalado y el vértice más cercano),
luego, resolvemos signos en la primera ecuación y queda:
c + a = 50
c - a = 2,
resuelves el sistema de ecuaciones y tienes: c = 26, a = 24,
luego, con la relación entre semiejes de una Hipérbola tienes:
b = √(c2 - a2) = √(262 - 242) = √(100) = 10,
y la ecuación de la Hipérbola queda:
x2/242 - y2/102 = 1,
resuelves denominadores y llegas a:
x2/576 - y2/100 = 1.
Luego, tienes todo lo que se necesita para indicar las coordenadas de los vértices, focos, vértices imaginarios, las ecuaciones de las asíntotas y la excentricidad de la Hipérbola.
Espero haberte ayudado.