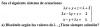-
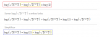
alguien podria resolverlo? (sé que está al revés pero no he podido solucionarlo)
Ángel
el 8/1/17elena
el 8/1/17Ángel
el 8/1/17elena
el 8/1/17 -
Antonio Silvio Palmitano
el 8/1/17Observa que tienes un sistema de tres ecuaciones lineales y de primer grado con tres incógnitas, por lo que comenzamos con plantear el determinante de la matriz del sistema, cuyos elementos son:
| λ 1 1 |
Δ = | 2 -λ 1 | = desarrollamos:
| 1 -1 λ |
= -λ3 - 2 + 1 + λ - 2λ + λ = reducimos términos semejantes:
= -λ3 - 1.
Luego, tenemos dos casos:
1) Si Δ ≠ 0, que corresponde a λ ≠ -1, tenemos que el rango de la matriz es igual a 3, y el sistema resulta ser compatible determinado con única solución.
2) Si Δ = 0, que corresponde a λ = -1, estudiamos el sistema con el método de Gauss, y para ello planteamos la matriz ampliada del sistema:
λ 1 1 λ+2
2 -λ 1 2
1 -1 λ λ
Reemplazamos λ = -1 y queda:
-1 1 1 1
2 1 1 2
1 -1 -1 -1
A la fila 3 le sumamos la fila 1 y queda:
-1 1 1 1
2 1 1 2
0 0 0 0
A la fila 2 le sumamos el doble de la fila 1 y queda:
-1 1 1 1
0 3 3 4
0 0 0 0
Luego, observa que el determinante de la submatriz cuyos elementos hemos remarcados es distinto de cero, por lo que tenemos que el rango de la matriz del sistema es igual a 2 al igual que el rango de la matriz ampliada, por lo que el sistema resulta ser compatible indeterminado con infinitas soluciones.
Espero haberte ayudado.
-
-------------------------------------------------------------------------------- COMBINATORIA --------------------------------------------------------------------------------
11.- Calcule la suma de todos los números de cuatro cifras distintas que se pueden formar con los dígitos 1, 3, 5 y 7.--->Rta.->106656
Calcule los números que cumplen con esas condiciones y son 24, pero no sabría como sumarlos.
Antonio Silvio Palmitano
el 8/1/17Observa que hay seis números cuya primera cifra es 1: 1357 1375 1537 1573 1735 1753;
observa que hay seis números cuya primera cifra es 3: 3157 3175 3517 3571 3715 3751;
observa que hay seis números cuya primera cifra es 5: 5137 5173 5317 5371 5713 5731;
observa que hay seis números cuya primera cifra es 7: 7135 7153 7315 7351 7513 7531.
Luego observa que todas las cifras ocupan todos los lugares en igualdad de condiciones, por lo tienes que cada una de ellas aparece seis veces en cada uno de los cuatro lugares, por lo que si sumas por separado en cada una de las cuatro cifras queda:
suma de las primeras cifras (millares): 6*1 + 6*3 + 6*5 + 6* 7 = 6*(1+3+5+7) = 6*16 = 96;
suma de las segundas cifras (centenas): 6*1 + 6*3 + 6*5 + 6* 7 = 6*(1+3+5+7) = 6*16 = 96;
suma de las terceras cifras (decenas): 6*1 + 6*3 + 6*5 + 6* 7 = 6*(1+3+5+7) = 6*16 = 96;
suma de las cuartas cifras (unidades): 6*1 + 6*3 + 6*5 + 6* 7 = 6*(1+3+5+7) = 6*16 = 96;
Luego, la suma de los veinticuatro números del conjunto queda:
S = 96*1000 + 96*100 + 96*10 + 96*1 = 96*(1000 + 100 + 10 + 1) = 96*1111 = 106656.
Espero haberte ayudado.
-
La juventud de un hombre sabio duró 1/6de su vida . se dejó barba despues de 1/12 mas .despues de 1/7 de su vida se casó. cinco años despues tuvo un hijo . esta vivió exactamente la mitad de tiempo que su padre, y el hombre sabio murio cuatro años despues. ?cuantos años tania al morir?Antonio Silvio Palmitano
el 8/1/17Llamemos x a la edad en años que tenía el sabio al fallecer.
Luego tienes una tabla de momentos en la vida del sabio:
0: nacimiento
x/6: terminó su juentud
x/6 + x/12 = x/4: se dejó barba
x/4 + x/7 = 11x/28: se casó
11x/28 + 5: tuvo un hijo (observa que el padre y el hijo vivieron ambos a la vez x/2 años)
11x/28 + 5 + x/2 + 4 = 25x/28 + 9: falleció (por lo que vivió 25x/28 + 9 años)
Luego, tenemos la ecuación:
x = 25/28x + 9, hacemos pasaje de término y queda:
3x/28 = 9, hacemos pasaje de factor como divisor y queda:
x/28 = 3, hacemos pasaje de divisor como factor y llegamos a:
x = 84 años.
Observa que el sabio:
terminó su juventud a los 18 años,
se dejó barba a los 21 años,
se casó a los 33 años,
tuvo un hijo a los 38 años,
fallece su hijo cuando la edad del sabio era 80 años,
falleció a los 84 años,
y observa que su hijo vivió: 84 - 38 = 42 años, que es la mitad del tiempo de vida del sabio.
Espero haberte ayudado.
-
Alguien me puede ayudar con este ejercicio. Simplifique la siguiente expresión dando el valor de Z en forma exponencial
(e^((pi/4)*i)-3-i)/z = i^7
Antonio Silvio Palmitano
el 8/1/17Tienes la ecuación:
( eiπ/4 - 3 - i )/z = i7,
observa que i7 = i4*i3 = 1*(-i) = -i, reemplazamos y queda:
( eiπ/4 - 3 - i )/z = -i, hacemos pasaje de divisor como factor y queda:
eiπ/4 - 3 - i = -iz, expresamos el primer término del primer miembro en forma trigonométrica, y luego en forma binómica y queda:
√(2)/2 + i√(2)/2 - 3 - i = - iz, dividimos en todos los términos de la ecuación por -i y queda:
(√(2)/2)/(-i) + i√(2)/(-2i) - 3/(-i) - i/(-i) = z, resolvemos en cada término y queda:
i√(2)/2 - √(2)/2 - 3i + 1 = z, agrupamos términos y queda:
(1 - √(2)/2) + i(-3 + √(2)/2) = z (observa que la parte real es positiva y la parte imaginaria es negativa, por lo que z pertenece al cuarto cuadrante).
Luego, planteamos:
|z|2 = (1 - √(2)/2)2 + (-3 + √(2)/2)2 = 1 - √(2) + 1/2 + 9 - 3√(2) + 1/2 = 11 - 4√(2); luego tenemos: |z| = √( 11 - 4√(2) ) ≅ 2,31.
tan(θ) = (-3 + √(2)/2)/(1 - √(2)/2) ≅ -7,8284, luego tenemos:
θ = arctan( (-3 + √(2)/2)/(1 - √(2)/2) ) ≅ -82,72° + 360° = 277,28° = (277,28/180)π = 1,54π radianes.
Luego, la expresión del número complejo z en forma exponencial queda:
z = |z|eiθ≅ 2,31ei1,54π.
Espero haberte ayudado.
-
Echadme una mano con está ecuación TRIGONOMÉTRICA porfa:
sen6x-2sen4x+sen2x=0
Antonio Silvio Palmitano
el 8/1/17Puedes emplear la sustitución (cambio de incógnita): w = 2x (1), luego sustituyes y la ecuación queda:
sen(3w) - 2sen(2w) + sen(w) = 0, haces pasaje de término y queda:
sen(3w) + sen(w) = 2sen(2w) (2).
Luego, puedes aplicar la identidad de transformación en producto en el primer miembro:
sen(3w) + sen(w) = 2sen( (3w+w)/2 )*cos( (3w-w)/2 ) = 2sen(2w)*cos(w),
luego sustituyes en la ecuación señalada (2) y queda:
2sen(2w)*cos(w) = 2sen(2w), haces pasaje de término y queda:
2sen(2w)*cos(w) - 2sen(2w) = 0, extraes factor común y queda:
2sen(2w)*( cos(w) - 1 ) = 0, luego, por anulación de un producto tienes dos opciones:
1)
2sen(2w) = 0, haces pasaje de factor como divisor y queda:
sen(2w) = 0, sustituyes según la ecuación señalada (1) y queda:
sen(4x) = 0, que conduce a:
4x = k*π, de donde tienes: x = k*π/4, con k ∈ Z.
2)
cos(w) - 1 = 0, haces pasaje de término y queda:
cos(w) = 1, sustituyes según la ecuación señalada (1) y queda:
cos(2x) = 1, que conduce a:
2x = 2k*π, de donde tienes: x = k*π, con k ∈ Z, que son soluciones contenidas en la opción anterior.
Espero haberte ayudado.
-
¿Alguna ayuda en este problema?
Efectúe la suma alfa/beta/alfa/beta/alfa/beta(base 12)+alfa/beta/alfa/beta/alfa(base 12).
Sin pasarlo todo a base 10 y sumar.
Gracias!
Sandra López Gómez
el 8/1/17Ángel
el 8/1/17alfa(posición1)/beta(p.2)/alfa(p.3)/beta(p.4)/alfa(p.5)/beta(base 12)(p.6) + alfa(p.1)/beta(p.2)/alfa(p.3)/beta(p.4)/alfa(base 12)(p.5)
-----------> alfa/beta/alfa/beta/alfa/beta(base 12): α 3 / β2*β12
Para obtener el numerador multiplicamos los de posición impar (leyendo de arriba a abajo normalmente, de izda a derecha en tu caso): alfa*alfa*alfa= α 3
Para obtener el denominador multiplicamos los de posición par: beta*beta*beta12= β2*β12
-----------> alfa/beta/alfa/beta/alfa(base 12): α2*α12 / β2
Para obtener el numerador multiplicamos los de posición impar: alfa*alfa*alfa12= α2*α12
Para obtener el denominador multiplicamos los de posición par: beta*beta= β2
ENTONCES LA SOLUCIÓN ES LA SUMA DE AMBAS PARTES:
α 3 / β2*β12 + α2*α12 / β2
Ángel
el 8/1/17Sandra López Gómez
el 12/1/17Gracias, creo que ya entendí como se hace. En base 12, alfa vale 10 y beta vale 11.
Si alfa+beta=10+11=21, pero como estamos en base 10, solo podemos llegar hasta beta, por tanto: 21-12=9, y me llevaría 1, y así sucesivamente, siendo el resultado: beta/alfa/alfa/alfa/alfa/9 en base 12.
-
El ejercicio pide estudiar la convergencia de la sucesión, llevo un buen rato intentándolo por el criterio de Raabe y no me sale...
Ángel
el 8/1/17Lfdelriolopez
el 8/1/17Conozco el teorema de Raabe y cómo se aplica, y concretamente la pagina a la que me has dirigido, el problema en sí es el ejercicio que en uno de los pasos del criterio de Raabe me quedo atascado, y no es por no saber el funcionamiento de dicho criterio, ya que he hecho mas de una docena de ellos sin ningún problema