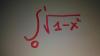-
Hola de nuevo, me gustaría que me ayudaran con este problema de fracciones:
Una pelota, al caer al suelo rebota hasta los 3/8 de altura desde la que se suelta. Si se deja caer desde 1024cm ¿a qué altura llegará tras el tercer bote?
mis dudas son : 1: ¿los 3/8 de altura corresponden al primer bote? 2: ¿cómo consigo averiguar el porcentaje del tercer bote?
la solución al problema debe ser 54cm "según el ejercicio corregido".
MUCHAS GRACIAS!
Álvaro Reverte
el 7/1/17Hola Alexandra.
Lo que te quiere decir el problema es que la pelota volverá a subir a los 3/8 de la última altura a la que estuvo, y eso se repite siempre. Es decir...
Sea a1=1024 cm. (la altura inicial), entonces a2= 3/8 · a1 y a3= 3/8 · a2 y a4= 3/8 · a3... es decir, cualquier altura an= 3/8 · a1, por lo que estamos ante una progresión ¿_______?
Por lo que has de pensar cuántas veces actúa ese "3/8" en el salto que te piden. Ten mucho cuidado y razona quién sería la altura después del tercer bote en el planteamiento que he hecho. ¿Sería a3?
Espero haberte ayudado.
SB!!
-
-
Antonio Silvio Palmitano
el 7/1/17Tienes la integral, para evaluar entre 0 y 1:
I = ∫ √(1 - x2) dx,
aplicas la sustitución trigonométrica:
x = senw (observa que para x = 0 tienes w = 0, y para x = 1 tienes w = π/2), de donde tienes: dx = cosw*dw, sustituyes y queda:
I = ∫ √(1 - sen2w)*cosw*dw = aplicas identidad trigonométrica = ∫ cosw*cosw*dw = ∫ cos2w dw,
luego, aplicas la identidad trigonométrica: cos2w = 1/2 + (1/2)cos(2w), sustituyes y queda:
I = ∫ ( 1/2 + (1/2)cos(2w) ) dw = [ (1/2)w + (1/4)sen(2w) ], luego evaluamos con la Regla de Barrow entre 0 y π/2 y queda:
I = (π/4 + 0) - (0 + 0) = π/4.
Espero haberte ayudado.
-
Buenos días,
estoy teniendo problemas con la siguiente ecuación trigonométrica:
tg x = √2 · cos x
He cambiado la tg por sen/cos y después he cambiado el sen por √(1-cos2x). Después he pasado el cos x multiplicando a √2 · cos x y he puesto √2 · 2 · cos x. Finalmente he quitado la raíz de √(1-cos2x) elevando los dos lados y me ha dado 1 - cos2 x = 8 cos2 x. Por último la solución me dado cos x = +-(1/3). ¿Lo he hecho bien?
Gracias.
Antonio Silvio Palmitano
el 7/1/17Tienes la ecuación trigonométrica:
tanx = √(2)*cosx, (observa que el coseno y la tangente tienen el mismo signo), elevas al cuadrado en ambos miembros y queda:
tan2x = 2*cos2x, aplicas la identidad trigonométrica de la tangente como sugieres y queda:
sen2x/cos2x = 2*cos2x, haces pasaje de divisor como factor, aplicas la identidad fundamental para el seno como sugieres y qeuda:
1 - cos2x = 2*(cos2x)2, aplicas la sustitución (cambio de incógnita): w = cos2x y queda:
1 - w = 2*w2, haces pasaje de término, ordenas términos y queda:
-2*w2 - w + 1 = 0, multiplicas en todos los términos de la ecuación por -1 y queda:
2*w2 + w - 1 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son: w1 = 1/2 y w2 = -1, por lo que tenemos dos opciones:
1) w = cos2x = 1/2, de donde tenemos dos opciones:
1a) cosx = √(2)/2, que corresponde a: x = π/4 = 45° (recuerda que el coseno y la tangente tienen las dos signos positivos en el primer cuadrante);
1b) cosx = -√(2)/2, que corresponde a: x = 3π/4 = 135° (recuerda que el coseno y la tangente tienen las dos signos negativos en el segundo cuadrante).
2) w = cos2x = -1, que no tiene solución real.
Espero haberte ayudado.
-
----------------------------------------------------------------------------------- COMBINATORIA -----------------------------------------------------------------------------------
Supóngase que se tienen 3 pilas de pelotas iguales, rojas, azules y verdes, donde cada pila contiene al menos 10 pelotas.
a)¿De cuántas maneras se pueden seleccionar 10 pelotas?-------------------------------------------------------------------------------------66b)¿De cuántas maneras se pueden seleccionar 10 pelotas, si debe tenerse, a lo sumo, una roja?---------------------------21
c)¿De cuántas maneras se pueden seleccionar 10 pelotas, si las rojas deben ser el doble de las verdes?--------------¿3 ó 4?
Antonio Silvio Palmitano
el 7/1/17Consideremos que tenemos una población de tres elementos (colores), de los que tenemos que elegir diez, sin orden y con repetición.
a) Tenemos por lo tanto: n = 3 (rojo, azul, verde), de los que elegimos en grupos de k = 10, por lo que planteamos combinaciones de tres elementos tomados de a diez, con repetición, a partir de la expresión: Cr(n,k) = C(n+k-1,k) (revisa tus apuntes de clase):
Cr(3,10) = C(3+10-1,10) = C(12,10) = 12! / 10!2! = 66.
b) Tenemos dos subconjuntos: elecciones con cero pelotas rojas (N0) y elecciones con una pelota roja (N1), por lo que calcularemos cada caso por separado para luego sumar y obtener el total (N):
1) Observa que tenemos dos elementos (azul, verde) para elegir diez, sin orden y con repetición, por lo que planteamos:
N0 = Cr(2,10) = C(2+10-1,10) = C(11,10) = 11! / 10!1! = 11.
2) Observa que tenemos una pelota roja desde el vamos, por lo que tenemos dos elementos (azul, verde), para elegir nueve, sin orden y con repetición:
N1 = Cr(2+9-1,9) = C(10,9) = 10! / 9!1! = 10.
Luego, tenemos en total:
N = N0 + N1 = 11 + 10 = 21.
c) Observa que tenemos tres casos posibles solamente:
1) elegimos 2 rojas, 1 verde, 6 azules,
2) elegimos 4 rojas, 2 verdes, 4 azules,
3) elegimos 6 rojas, 3 verdes, 1 azul;
por lo tanto concluimos:
N = 3.
Espero haberte ayudado.
-
Hola buenos días! intento resolver un problema de fracciones: una bolsa tiene 24 bolas, de ellas 1/4 son blancas.Sin sacar ninguna ¿Cuántas bolas blancas debo añadir para que éstas sean la mitad de la bolsa? haciendo un dibujo para entender mejor el problema me da como resultado doce bolas blancas, pero no sé cómo explicarlo de manera matemática. muchas gracias!
César
el 7/1/17Antonio Silvio Palmitano
el 7/1/17Continuamos a partir del planteo del colega César, por lo que tenemos al inicio 6 bolas blancas de un total de 24.
Si llamas x a la cantidad de bolas blancas que debes agregar, puedes plantear:
Nueva cantidad de bolas blancas / Nueva cantidad total = 1/2, luego tienes:
(6 + x)/(24 + x) = 1/2, haces pasajes de divisores como factores y queda:
2*(6 + x) = 1*(24 + x), distribuyes en ambos miembros y queda:
12 + 2x = 24 + x, haces pasajes de términos y queda:
2x - x = 24 - 12, resuelves en ambos miembros y llegas a:
x = 12.
Espero haberte ayudado.
-
Buenas noches unicoos,quisiera que me aclaren una duda,la Suma de Riemman puedo representar de cualquiera de estas formas?
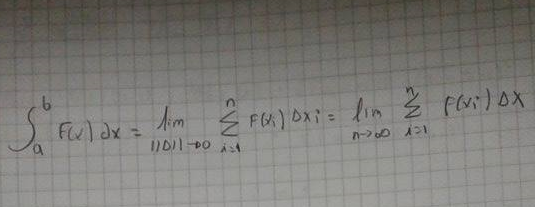
O la Suma de Riemman tiene otra fórmula?
Antonius Benedictus
el 7/1/17https://bjglez.webs.ull.es/06-integral.pdf
Aquí lo tienes muy bien explicado.
-