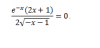-
Alejandro Legaspe
el 14/12/16El si y solo si implica dos proposiciones, a saber, la primera que si (a+c) /(b+c)=a/b entonces a=b o c=0 y la otra es que si a=b o c=0 entonces (a+c) /(b+c)=a/b, para desmotrar las dos de un jalon podemos poner el si y solo si, es decir que los pasos siguientes son tanto validos como se lee a continuación como de abajo hacia arriba:
Sabemos que (a+c) /(b+c)=a/b, con b es distinto de 0 y distinto de -c
⇔b(a+c) = a(b+c)
⇔ab+bc=ab+ac
⇔ab+bc-ab-ac=0
⇔ab -ab + bc -ac=0
⇔0+bc-ac=0⇔bc-ac=0
⇔c(b-a)=0
⇔ c=0 o b-a=0 es decir, b=a -
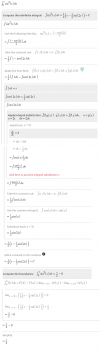
Buenas, ¿podría alguien ayudarme a resolver esta ecuación? Si puede ser, con los pasos que estoy un poco oxidado con las ecuaciones.
el resultado que obtengo es x=√(-2e-1)/4, pero diría que lo tengo mal:
Antonio Silvio Palmitano
el 14/12/16Primero, observa que el denominador debe ser distinto de cero y que, además, el argumento de la raíz cuadrada debe ser positivo, por lo tanto planteamos:
-x -1 > 0, hacemos pasaje de término y queda:
-x > 1, multiplicamos en ambos miembros por -1 (recuerda que cambia la desigualdad, por ser un número negativo):
x < -1 (1),
por lo que tenemos que las soluciones de la ecuación deben ser números estrictamente menores que -1.
Luego, haces pasaje de divisores como factores y queda:
e-x(2x + 1) = 0*2√(-x - 1), resolvemos el segundo miembro y queda:
e-x(2x + 1) = 0, aplicamos propiedad de los factores con exponente negativo y queda:
(2x + 1)/ex = 0, luego hacemos pasaje de divisor como factor (recuerda que ex es estrictamente positivo) y queda:
2x + 1 = 0*ex, resolvemos el segundo miembro y queda:
2x + 1 = 0, hacemos pasaje de término y queda:
2x = -1, hacemos pasaje de factor como divisor y llegamos a:
x = -1/2, que no es solución válida de la ecuación porque no cumple la inecuación señalada (1),
por lo que concluimos que la ecuación del enunciado no tiene solución.
Espero haberte ayudado.
Luis Cano
el 14/12/16El cociente es 0 cuando el numerador es 0. Es claro que e^(-x) es diferente de 0 para toda x y 2x+1=0 cuando x=-1/2. Intuitivamente esa seria la solución, pero observa que el dominio de dicha función es x<-1 y la solución hallada no esta en ese intervalo. Por lo que no hay soluciones en los reales.
O dicho de otra manera, cuando evalúas en x=-1/2 obtienes una raíz compleja y supongo estas trabajando en los reales. Cualquier duda comenta :)
-
Argenis Briceño
el 14/12/16Luis Cano
el 14/12/16Yo no se para que colocan capturas cuando pueden pasarte el link de la pagina: https://es.symbolab.com/. Dale un buen uso :)
Antonio Silvio Palmitano
el 14/12/16 -
Hola buena, mi duda es teórica, que diferencia hay entre calcular un límite y estudiar un límite ?
En dicho caso, un ejercicio me pedía estudiarlo e hice el límite y me daba 0/0 ( INDET ) sin embargo en su resolución solo calculaba los límites laterales, dejo aqui puesto el ejercicio
L x->0 de (x*senx)/(x)
Gracias
Antonio Silvio Palmitano
el 14/12/16Observa que el límite es indeterminado, ya que el numerador (N) tiende a cero, y el denominador (D) tiende a cero.
Luego, debemos estudiarlo, a fin de llegar a su resultado.
En el ejercicio del enunciado tienes:
Lím(x→0) (x*senx)/x = simplificamos = Lím(x→0) senx = evaluamos = 0.
En este caso, hemos estudiado el límite (hemos podido "salvar la indeterminación"), lo hemos calculado y es igual a cero.
Espero haberte ayudado
-
Hola me pueden ayudar con este ejercicio es de estadística distribución normal
El área de la curva normal estándar entre (-2.35<z<-0.50) es 0.3179.
necesito ver si es verdadero o falsa pero no entiendo como hacerla con las formulas......
Antonio Silvio Palmitano
el 14/12/16Debes tener en cuenta que hay dos tipos de tablas:
1) Las que expresan el valor del área bajo la curva normal ("campana de Gauss"), para todo valor de z, tanto negativo como positivo;
2) las que expresan el valor del área bajo la curva normal, para el intervalo que va desde z = 0 hasta un valor de z que sea mayor que cero.
Por lo tanto, observa que tu intervalo tiene extremos negativos, por lo que, según sea la tabla, se calculan:
1) A = Φ(-0,50) - Φ(-2,35) = buscas los valores y resuelves;
2) A = ( 1 - Φ(0,50) ) - ( 1 - Φ(2,35) ) = 1 - Φ(0,50) - 1 + Φ(2,35) = - Φ(0,50) + Φ(2,35) .
Recuerda que la gráfica de la curva normal es simétrica con respecto al eje OY, por lo que se cumple:
Φ(-a) = 1 - Φ(a),
donde Φ(a) expresa el valor del área de la región que se encuentra entre el eje OX y la curva normal:
1) desde - infinito hasta a, con a mayor que cero;
2) desde 0 hasta a, con a mayor que cero.
Espero haberte ayudado.
-
Alguien podría darme alguna indicación de como hacer este problema? Gracias:
Siendo D la región limitada por el eje OX i el arco de cicloide x=t-sint, y=1-cost, t varia entre 0 i 2π . Calcular el valor de:
∫∫D (y2) dxdy
Antonio Silvio Palmitano
el 14/12/16Puedes integrar primero con respecto a y, y luego plantear la integral con respecto a x:
A = ∫∫D y2 dydx = ∫ [y3/3] dx = (1/3) ∫ [y3] dx,
luego evalúas con la Regla de Barrow entre y = 0 e y(t) = 1 - cost, sustituyes dx = x ' (t)dt, y queda:
A = (1/3) ∫ (1 - cost)3 (1 - cost) dt = (1/3) ∫ (1 - cost)4dt,
Luego queda que resuelvas la integral, para lo que deberás revisar tus apuntes de clase, o lo que es muy recomendable, puedes mirar los vídeos sobre integración de funciones trigonométricas.
Haz el intento, y si te es preciso, no dudes en volver a consultar.
Espero haberte ayudado
-
Buenas, mi problema es el siguiente:
El número promedio de despidos que una empresa realiza al año es de 1,5 trabajadores. Determine la probabilidad de que.
a) En un período de 2 años se despidan 3 trabajadores.
b) En 6 meses se despida 1 solo trabajdor.
c) En un año no haya despidos.
He pensado que sería lógico usar distribución normal pero debido a que no me dan la desviación estándar no sería viable. ¿Cómo se abordaría este problema? Creo que la respuesta es sencilla y tan solo me complico.
Ángel
el 14/12/16Hazlo con la distribución muestral de diferencia de proporciones
http://www.itchihuahua.edu.mx/academic/industrial/estadistica1/cap01c.html
(segundo ejemplo)
Antonio Silvio Palmitano
el 14/12/16Observa que tienes una variable aleatoria discreta:
X = "cantidad de trabajadores despedidos en un periodo de tiempo", que puede tomar valores: 0, 1, 2, 3, ...
Puedes plantear por medio de la distribución de Poisson (p(X=k) = e-λ * λk / k!, con k = 0, 1, 2, 3, ...),
con parámetro:
a) λ = 1,5*2 = 3 para periodos de dos años,
b) λ = 1,5/2 = 0,75, para periodos de medio año,
c) λ = 1,5 para periodos de un año.
Espero haberte ayudado.
-
Demuestra q los planos (pi): 2X+3y-4z=6 y (pi)': -3X+4y-2z=-2, no son paralelos y calcula sus planos bisectores
Javier Martin Mena
el 13/12/16
A₁x + B₁y+ C₁z = D₁ ⇒ Vector normal n₁ = (A₁; B₁; C₁)
A₂x + B₂y+ C₂z = D₂ ⇒ Vector normal n₂ = (A₂; B₂; C₂)Los planos son paralelos si son paralelos los vectores normales. Dos vectores son paralelos si los cocientes entre sus componentes homólogas son iguales.
n₁ || n₂ ⇔ A₁/A₂ = B₁/B₂ = C₁/C₂
con A₂ ≠ 0; B₂ ≠ 0; C₂ ≠ 0. Si alguna fuese cero, su homóloga también debe ser cero y no se escribe el cociente entre esas componentes, solamente se comparan los no nulos.Para los bisectores sustituir:
-
Buenas, me podría alguien ayudar con el ejercicio "C"
La respuesta es :
PD: podría alguien explicarlo paso a paso por favor, no me sale el Radio 2.
Gracias!!
Antonio Silvio Palmitano
el 13/12/16Observa que el argumento de la raíz cuadrada debe ser mayor o igual que cero, por lo que planteamos:
- x2 - y2 + 4x ≥ 0,
multiplicamos en todos los términos de la inecuación por -1 (observa que cambia la desigualdad) y queda:
x2 + y2 - 4x ≤ 0, ordenamos términos, sumamos en ambos miembros 4 y queda:
x2 - 4x + 4 + y2 ≤ 4,
factorizamos el trinomio cuadrado perfecto, al que hemos remarcado, y queda:
(x - 2)2 + y2 ≤ 4,
luego observa que la inecuación corresponde a un disco circular cerrado (incluye a su frontera) con centro en el punto de coordenadas: C(2,0), cuyo radio es: R = √(4) = 2. El disco es acotado y convexo.
Luego, el dominio de la función queda expresado:
D = {(x,y) ∈ R2/ (x - 2)2 + y2 ≤ 4}.
Espero haberte ayudado.
-
Hola, mi duda no es especifica, es un poco un grito desesperado de intentar guiarme el caso es que por ciertos incovenientes provisionales deje de ir a clase a finales de 1 de la eso( he de decir que he vuelto por primera vez a acudir a clase regularmente hace un mes), a dia de hoy estoy en 4 aprobando los cursos que hay entre medias de chirigota o bien haciendo uso de maneras no muy legitimas para aprobar examenes, como os podeis imaginar mi base es ridicula, he dejado de ir a clase de matematicas basicamente por que todo lo que hablan y estan dando en clase me faltan muchos conocimientos previos para si quiera poder disvisar una luz en tunel, y tampoco voy a preguntar ya que estaria totalmente fuera de contexto si ni si quiera comprendo que hay en la pizarra. El caso es obviamente me gustaria poder superar con exito la asignatura, el itinerario que hay marcado para matematicas en el instituto que voy es este, por lo que mi pregunta es ¿ Viendo este itinerario, que podría hacer para poder llegar al nivel? ¿Por donde tengo que empezar y transcurrir?¿Como es de complicado ponerme al día? ¿Estoy muy lejos? Por supuesto son bien recibidos todos los video de unicoos que me puedan ayudar en mi tarea muchas gracias de antemano y un saludo.
Bloque 1º: Números
Expresión de los números racionales mediante fracciones, porcentajes y formas decimales.
Números irracionales. Números reales.
Intervalos. Valor absoluto. Representación de conjuntos numéricos en la recta real.
Expresión aproximada de un número real. Redondeo. Errores. Cálculo con aproximaciones.
Potencias de exponente natural, entero y fraccionario.
La notación científica. Operaciones sencillas con números en notación científica con y sin calculadora
Radicales. Forma exponencial de los radicales.
Operaciones con radicales. Radicales semejantes.
Magnitudes directa e inversamente proporcionales.
Repartos directa e inversamente proporcionales.
Porcentajes. Porcentajes sucesivos. Aumentos y disminuciones porcentuales.
Porcentajes en la economía. Interés simple. Interés compuesto.
Bloque 2º. Álgebra
Lenguaje algebraico. Polinomios. Suma, resta, producto y cociente de polinomios. Productos notables. Regla de ruffini
Descomposición factorial de un polinomio. Raíces de un polinomio.
Fracciones algebraicas. Operaciones. Simplificación de fracciones algebraicas.
Resolución
de ecuaciones con denominadores, de segundo grado, bicuadradas,
radicales con un radical, de grado superior a tres mediante
factorización y exponenciales sencillas.Inecuaciones de primer grado. Sistemas de inecuaciones de primer grado.
Sistemas de ecuaciones lineales (de dos y tres ecuaciones e incógnitas) y no lineales de dos ecuaciones y dos incógnitas.
Resolución de problemas mediante el planteamiento de ecuaciones, inecuaciones y sistemas de ecuaciones.
Bloque 3º. Funciones y gráficas
Funciones dadas por tablas, gráficas y expresión analítica.
Interpretación de la gráfica de una función.
Dominio y recorrido de una función.
Características
de las gráficas: puntos de corte con los ejes, signo, crecimiento y
decrecimiento, máximos y mínimos, continuidad, simetrías y periodicidad.
Idea intuitiva de asíntotas horizontales y verticales.Funciones lineales. Pendiente de una recta. Función de proporcionalidad y función constante.
Funciones definidas mediante "trozos" de rectas. Función valor absoluto.
Funciones cuadráticas. Elementos de la parábola: Vértice, eje de simetría, puntos de corte con los ejes.
La función de proporcionalidad inversa. La hipérbola.
Funciones racionales. Idea intuitiva y con la calculadora de asíntotas horizontales y verticales.
Las funciones exponenciales. El número e.
Problemas de aplicación de funciones a situaciones de las ciencias naturales, de la economía,..etc.
Bloque 4º. Estadística y Probabilidad
Estadística unidimensional. Tablas de frecuencia. Gráficos estadísticos.
Parámetros de centralización, de dispersión y de posición.
Técnicas de recuento. Diagrama de árbol. Combinatoria.
Factoriales y números combinatorios. Binomio de Newton.
Sucesos aleatorios. Álgebra de sucesos. Sucesos compatibles, incompatibles y contrarios.
Asignación de probabilidades a los sucesos. Regla de Laplace. Propiedades.
Experiencias compuestas dependientes e independientes. Probabilidad condicionada.
Cálculo de probabilidades en experimentos compuestos. Tablas de contingencia.
Bloque 5º. Geometría
Relación de semejanza. Teorema de Tales.
Aplicación de la semejanza y el teorema de Pitágoras para la obtención indirecta de medidas.
Cálculo de longitudes, áreas y volúmenes.
Razones trigonométricas en triángulos rectángulos. Relaciones entre las razones trigonométricas.
Resolución de triángulos rectángulos. Uso de la calculadora.
Aplicaciones de la trigonometría. Cálculo de una altura de pie accesible e inaccesible.
Vectores: Elementos de un vector. Vector dado por su origen y extremo. Representación gráfica.
Coordenadas de un punto. Representación gráfica. Punto medio de un segmento. Distancia entre dos puntos.
Ecuaciones punto-pendiente, implícita y explícita de la recta.
Posiciones relativas de dos rectas. Punto de intersección
Ángel
el 14/12/16Tienes que ver todos los vídeos de matemáticas de unicoos de 1ESO-1ºBachillerato (empezando por 1º de la ESO y sin pasar a otro vídeo si no has comprendido TODO) y realizar los ejercicios al final de cada vídeo, pregunta CUALQUIER duda que tengas aquí en el foro.
(de 1º de Bachillerato no hace falta que veas derivadas e integrales por lo que he visto en tu temario)
No es difícil, pero tienes que ir con calma y echar todos los días un ratito
Ánimo, aquí estamos nosotros para guiarte en lo que no entiendas
Sí.
el 14/12/16Muy buenas "Maths", lo primero darte un millon de gracias por responder a tan profunda y costosa pregunta y tomarte el tiempo de leerla al completo, seguire tus encomendaciones, en un principio buscaba algo mas "practico" para poder empezar a salvar el curso desde ya, pero creo que tu opcion es mas sensata, ya que es mejor emplear algo mas de tiempo y tener una base ferrea y unos conocimientos solidos que poder ampliar poco a poco. ¿Creés que de aqui a la vuelta de las navidades podria conseguir alcanzar el nivel del curso?, ¿y con ello poder coger las riendas de la 2 evaluación?. Habia empezado a mirar videos de ecuaciones de primer grado, pero parece ser que hay que echar la vista algo mas para atras .
Una vez mas un millon de gracias, que tengas un muy buen día.