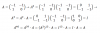Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

fabian
el 13/12/16

Hola tengo dificultades con este ejercicio de geometría analítica no consigo plantearlo.
La hipotenusa de un triangulo rectángulo es el segmento que une (0,0) y (4,0)
a) Determinar la ecuación del lugar geométrico del tercer vértice P
b) Trazar la gráfica del lugar geométrico analizando previamente: intercepciones Y simetrías con respecto a ejes coordenados y extensión de la curva

NO CONSIGO PLANTEARLO POR MAS QUE HAGO EL DIBUJO

De antemano gracias

••0 voto/s
•
Antonius Benedictus
el 13/12/16

•0 voto/s
•

Cancelar
Jonathan Yañez
el 13/12/16

--------------------------TRIGONOMETRIA---------------------
56.- Encontrar todos los valores de X E R que verifiquen la siguiente ecuación:
sen(2x+π) - (cos^2)x + (sen^2)x + cos(2x) = 1

••0 voto/s
•
Antonius Benedictus
el 13/12/16

•1 voto/s
•
César
el 13/12/16
Va

•1 voto/s
•
Jonathan Yañez
el 14/12/16
Perdón pero no se de las dos cual es la correcta.

•0 voto/s
•
Antonius Benedictus
el 14/12/16
La correcta es la de César. Yo me despisté, pues sin (a+π)=-sin a
Disculpa.

•1 voto/s
•
Jonathan Yañez
el 15/12/16
Gracias a los dos!!!

•0 voto/s
•

Cancelar
nico jai
el 13/12/16

Buenas tardes quisiera saber si el siguiente ejercicio que escribiré esta bien: 3lx-2l-2>1 caso a) x-2<0 ----> -3lx-2l-2>1
a lo que me refiero que pasa con el -2 que esta restando pasa algo aunque le ponga un - adelante del 3 ?

••0 voto/s
•
Antonio Silvio Palmitano
el 13/12/16
Tienes la inecuación:
3|x - 2| - 2 >1, haces pasaje de término y queda:
3|x - 2| > 3, multiplicas en ambos miembros por 1/3 (observa que no cambia la desigualdad) y queda
|x - 2| > 1, luego tienes dos opciones:
a) si x - 2 < 0, que conduce a x < 2, entonces la inecuación queda:
-(x - 2) > 1, distribuyes en el primer miembro y queda:
-x + 2 > 1, haces pasaje de término y queda:
-x > -1, multiplicas en ambos miembros por -1 (observa que si cambia la desigualdad) y queda:
x <1,
luego, el intervalo solución para esta opción (cuyos elementos verifican las dos inecuaciones remarcadas) queda: S_a = (-inf,1);
b) si x - 2 ≥ 0, que conduce a x ≥ 2, entonces la inecuación queda:
x - 2 > 1, haces pasaje de término y queda:
x > 3,
luego, el intervalo solución para esta opción (cuyos elementos verifican las dos inecuaciones remarcadas) queda: S_b = (3,+inf).
Luego, el intervalo solución de la inecuación del enunciado queda:
S = Sa u Sb = (-inf,1) u (3,+inf).
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Paula
el 13/12/16

Ayuda con esta derivada: f(x)=xe^x +1

••0 voto/s
•
DueFreitas
el 13/12/16
f ' (x) = e^x+x.e^x+0
f ' (x) = e^x(1+x) . Se utiliza la propiedad U.V tal que U =x y V=e^x y Derivada de una constante igual a Cero. para el 1 .

•1 voto/s
•

Cancelar
Pablo
el 13/12/16
1. Buenas hay un ejercicio q no entiendo me piden la matriz A^40 siendo la matriz A=(-1-1)↓ la matriz está formada por esos números. Cuando llegó a A³ me la matriz identidad y no se como seguir gracias..
(1 0)
••0 voto/s
•
Antonius Benedictus
el 13/12/16

•0 voto/s
•
Antonio Silvio Palmitano
el 13/12/16
¡Ya has hecho bien la parte más dura del ejercicio!
Porque es tal cuál dices: A³ = I₃.
Observa que el exponente lo puedes escribir: 40 = 3*13 + 1, luego tienes:
A⁴⁰ = A^3*13+1 = A^3*13*A¹ = (A³)¹³*A = (I₃)¹³*A = I₃*A = A.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Paula
el 13/12/16

Ayuda con esta integral indefinida por favor!!
Integral de ln(x+1)/(x+1)

••0 voto/s
•
Ángel
el 13/12/16

•1 voto/s
•
Marcos
el 13/12/16

•1 voto/s
•

Cancelar
Road FTW
el 13/12/16

Buenas, tenía dudas con estos ejercicios... uno es de una representación gráfica de una funcion, otro de matrices y otro de optimización. Si alguien es capaz de ayudarme lo agradecería, saludos

••0 voto/s
•
Antonius Benedictus
el 13/12/16

•1 voto/s
•
Antonius Benedictus
el 13/12/16

•1 voto/s
•

Cancelar
Carlos Muñoz
el 13/12/16

Hola, muy buenas me podrías ayudar en un ejercicio de trigonometría. Enunciado: Demostrar que la siguiente identidad se cumple:

••0 voto/s
•
Antonius Benedictus
el 13/12/16
Carlos, revisa el enunciado. A mí me da otra cosa.

•1 voto/s
•

Cancelar
Adrian
el 13/12/16

Buenas tardes, me ayudarían con este ejercicio, pude resolver la primer parte pero cuando me pide que use la misma fórmula para demostrar .....No se como plantear lo. Gracias

••0 voto/s
•
Guillem De La Calle Vicente
el 13/12/16

•1 voto/s
•
Antonio Silvio Palmitano
el 13/12/16
Observa que puedes escribir:
n³ = ∑(i=1,n) i³ - ∑(i=1,n-1) i³ = luego aplicamos la fórmula anterior y queda:
n³ = (1/4)n²(n + 1)² - (1/4)(n - 1)²n²
Luego observa en el primer término:
a) si n es par, entonces escribimos:
(1/4)n²(n + 1)² = ( (n/2)(n + 1) )²
que es el cuadrado del número natural (n/2)(n + 1) (observa que n/2 es un número natural)
b) si n+1 es par, entonces escribimos:
(1/4)n²(n + 1)² = ( n( (n+1)/2 )²
que es el cuadrado del número natural n( (n+1)/2 ) (observa que (n+1)2 es un número natural).
Luego observa en el segundo término:
a) si n es par, entonces escribimos:
(1/4)(n - 1)²n² = ( (n-1)n/2 )²
que es el cuadrado del número natural (n-1)n/2 (observa que n/2 es un número natural
b) sin n-1 es par, entonces escribimos:
(1/4)(n - 1)²n2 = ( ( (n-1)/2 )n )²
que es el cuadrado del número natural ( (n-1)/2 )n (observa que (n-1)/2 es un número natural.
Observa que en el primer término tenemos el cuadrado de un producto de números naturales consecutivos, por lo que uno de ellos es par y el otro es impar, y lo mismo ocurre en el segundo término.
Espero haberte ayudado.

•1 voto/s
•
Antonius Benedictus
el 13/12/16

•1 voto/s
•
César
el 13/12/16
Pues va otro

•1 voto/s
•

Cancelar
MG
el 13/12/16

ES una matriz 2x2. Me lo podría resolver? Graciaas 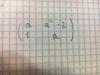-Estudia para qué valores de ''a'' no existe la matriz A a la inversa:

••0 voto/s
•
Gabriel
el 13/12/16
Hola MG, espero que esto te sirva de ayuda...
Para que no exista una matriz inversa, su determinante debe ser igual a cero, es decir, |A|=0.
Así que calculamos el |A|= a·a-(a²-2)·1=a²-a²+2=2, por lo que las "a" se nos anulan y tenemos que |A|=2, por lo que no existe valor de a perteneciente a los reales para que no exista su matriz inversa. Dicho de otra forma, la matriz A tiene siempre inversa, independientemente de lo que valga "a".
Saludos.

•1 voto/s
•

Cancelar