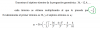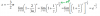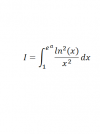-
-
Alex Domínguez
el 13/12/16Ángel
el 13/12/16Observa que
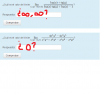
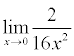 ya no es una indeterminación y ya no se le hace L'Hopital, porque queda "exactamente" 2/16*02= 2/0= infinito
ya no es una indeterminación y ya no se le hace L'Hopital, porque queda "exactamente" 2/16*02= 2/0= infinitoEntre las fórmulas para resolver este tipo de problema nos encontramos con: k/0=infinito infinito/0=infinito
***0/0 sí sería indeterminación y convendría usar L'Hopital seguramente
-
sus
el 13/12/16he de entender que donde pone r=1 está errado, ya que si la sucesión es 2, -6, 18... sabemos que la razón es -3. Porque a2/a1= -6/2 = -3 así como a3/a2= 18/-6= -3. A partir de ahí todo lo demás escrito debería tenerte ya sentido. repito, el único error que yo vi es poner r=1.
Ángel
el 13/12/16Yo también pienso que es el único error en la resolución que te daban, es r= -3, está claro
Y un pequeño apunte, aunque lo que pusiste en azul no tiene sentido, ya que tomaste r=1 erroneamente porque te lo daban como un mal dato
Aprovecho para decirte que 2*12-1=2*11=2 (y no 3 como pusiste tú)
-
Buenos días
Pueden decirme si hay alguna razon por la que se multiplica por -1/3 ? la potencia la entiendo. gracias
sus
el 13/12/16Hola Carlos, lo mismo que el anterior. En las sucesiones o progresiones geométricas, la razón que es valor por el cual se multiplica un termino para obtener sus siguiente se obtiene dividiendo siempre el "siguiente" entre el "anterior", es decir, a2/a1 o a3/a2 ...
En tu caso, -12/36 = -1/3 al igual que 4/-12= -1/3 por eso multiplicas por -1/3. Espero haberte ayudado, igualmente igual puedes revisar este video y te quedará más claro.
https://www.youtube.com/watch?v=UZDnLqEtE_8
Ángel
el 13/12/16Vamos a verlo con recursividad y así vas cogiendo más conceptos:
Es una sucesión recursiva, se utiliza el dato an para conocer el an+1
Datos: a1=36 an+1= -1/3*an (es lo que preguntabas, es un dato que te dan concreto, de este ejercicio, podrían haberte dicho cualquier otro coeficiente o razón)
a1+1= -1/3*a1 ------------------>a2=-1/3*36=-12
a2+1= -1/3*a2 ------------------>a3=-1/3*(-12)=4
a3+1= -1/3*a3 ------------------>a4=-1/3*(4)=-4/3
a4+1= -1/3*a4 ------------------>a5=-1/3*(-4/3)=4/9
a5+1= -1/3*a5 ------------------>a6=-1/3*(4/9)=-4/27
a6+1= -1/3*a6 ------------------>a7=-1/3*(-4/27)=4/81
-
-
APLICO TEOREMA FUNDAMENTAL Y SALE NO?
aplicandolo lelgo a e^a ln^2(e^a)/e^2a
RESPUESTA ES a=2, y el valor de I es -10e^-2+2
Antonio Silvio Palmitano
el 13/12/16Puedes plantear el método de integración por partes:
u = ln2(x), de donde tienes: du = 2lnx*dx/x
dv = dx/x2, de donde tienes; v = -1/x = - x-1.
Luego la integral queda:
I = ln2(x)*(- x-1) - ∫ (- x-1)*2lnx*dx/x =
= - x-1*ln2(x) + 2 ∫ lnx*x-2dx =
luego, puedes continuar la tarea (observa que la integral secundaria también se puede plantear con el método de integración por partes, con u = lnx, dv = x-2dx, etcétera).
Espero haberte ayudado.
-
Yo tengo una duda respeto a Gauss, es evitable en algun momento usar fracciones o siempre hay algun modo de evitar el uso de fracciones ?