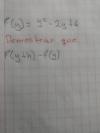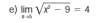-
como resolver f(1/x+h)-f(1/x)
Antonio
el 23/2/19 -
Antonio
el 23/2/19Antonio
el 23/2/19Al ser 1 por la derecha, es decir, números próximos al 1 por la derecha, es decir, números mayores que 1 pero muy próximos tenemos que x-1 serían números muy cerca al cero, pero mayores que el cero, es decir positivos.
Por lo tanto la división es positiva, pues el numerador es positivo y el denominador tb lo es por lo que te acabo de comentar
-
Muchas gracias Antonio, pero no entiendo por qué no importa el orden, porque el subconjunto abc es diferente que el subconjunto cba no? y si ponemos que no importa el orden estamos diciendo que esos dos subconjuntos son iguales, y el ejercicio me pide todos los posibles. ¿Entiendes mi duda? gracias otra vez y perdona pero es quo no entiendo
Antonio Silvio Palmitano
el 23/2/19Recuerda que cuando se define un conjunto, o subconjunto, por extensión solo hay que enumerar cuáles son sus elementos, sin repetirlos y sin importar el orden.
En el ejercicio que has consultado, los subconjuntos expresados en palabras son:
S1: subconjunto cuyos elementos son las letras A, B y C;
S2: subconjunto cuyos elementos son las letras A, B y D;
S3: subconjunto cuyos elementos son las letras A, C y D;
S4: subconjunto cuyos elementos son las letras B, C y D,
y observa que hemos planteado combinaciones:
C(4,3) = 4! / 3!*(4-3)! = 4! / 3!*1! = 4.
En cambio, si te hubiesen pedido en el enunciado: ¿cuántas palabras de tres letras (que tengan o no tengan sentido para la lengua castellana) con letras distintas, observa que por cada subconjunto tienes seis palabras posibles:
ABC, ACB, BAC, BCA, CAB y CBA para el primer subconjunto;
ABD, ADB, BAD, BDA, DAB y DBA para el segundo subconjunto;
ACD, ADC, CAD, CDA, DAC y DCA para el tercer subconjunto;
BCD, BDC, CBD, CDB, DBC y DCB para el cuarto subconjunto;
y observa que tienes 24 palabras posibles,
y que podrías haber planteado Variaciones Sin Repetición :
V(4,3) = 4! /(4-3)! = 4! / 1! = 24.
Y si te hubiesen pedido en el enunciado: ¿cuántas palabras de tres letras (que tengan o no tengan sentido para la lengua castellana), con repetición de letras, observa que tienes:
cuatro opciones para elegir la primera letra,
y por cada elección que hicieses tienes cuatro opciones para elegir la segunda letra,
y luego tienes a a su vez cuatro opciones para elegir la tercera letra,
por lo que tienes en total: 4*4*4 = 64 palabras posibles,
y observa que podrías haber planteado Variaciones Con Repetición:
Vr(4,3) = 43 = 64.
Espero haberte ayudado.
-
Hola a todos, alguien puede ayudarme con este ejercicio de combinatoria? EJERCICIO: CON LAS LETRAS A,B,C,D forma todos los subconjuntos posibles de tres elementos.
Cuando lo hizo en el colegio le salía de solución 4, pero no entiendo porque no tendríamos que usar la fórmula de variacion con repetición? por lo que entiendo el orden si importa porque la combinación "abc" es diferente que la combinación "cba" no? A mi me salen 64 formas en vez de 4
POr favorr si alguien me puede ayudar, tengo examen la semana que viene y no me aclaro
Antonio Silvio Palmitano
el 23/2/19Observa que tienes una población, formada por las letras: A, B, C y D, cuyo tamaño es: n = 4.
Observa que tienes que elegir tres elementos: k = 3, sin importar el orden de la elección y sin repetirlo, a fin de formar todos los subconjuntos posibles de tres elementos.
Luego, tienes dadas las condiciones para plantear la combinación de cuatro elementos tomados de a tres, por lo que puedes plantear la expresión:
C(4,3) = 4! / (3!*1!) = (4*3*2*1) / (3*2*1 * 1) = simplificas = 4;
por lo que puedes concluir que se pueden formar cuatro subconjuntos, cuyos elementos indicamos en secuencias en orden alfabético:
ABC , ABD , ACD y BCD.
Observa que para formar subconjuntos no interesa el orden, por lo que no se trata de una variación, y tampoco se puede repetir elementos (recuerda que los elementos de un conjunto no vacío son distintos entre sí).
Espero haberte ayudado.
-
aliguien q me pueda resolver esto por favor
1- Dado tgα = - 0,75 con 270°< α <360°. Deducir utilizando las fórmulas trigonométricas.
a) cosα b) cosecα
Antonio Silvio Palmitano
el 23/2/19Observa que el ángulo α pertenece al cuarto cuadrante, por lo que tienes que su coseno es positivo y su seno es negativo.
a)
Planteas la identidad del coseno en función de la tangente, y queda:
cos2α = 1 / (1 + tan2α), reemplazas el valor de la tangente en el segundo miembro, y queda:
cos2α = 1 / ( 1 + (-0,75)2 ), resuelves el denominador, y queda:
os2α = 1 / 1,5625, extraes raíz cuadrada positiva (recuerda el cuadrante) en ambos miembros, y queda:
cosα = 1/1,25, resuelves, y queda:
cosα = 0,8.
b)
Planteas la identidad del seno en función de la tangente, y queda:
sen2α = tan2α / (1 + tan2α), reemplazas el valor de la tangente en el segundo miembro, y queda:
sen2α = (-0,75)2 / (1 + (-0,75)2), resuelves el numerador y el denominador en el segundo miembro, y queda:
sen2α = 0,5625 / 1,5625, resuelves el segundo miembro, y queda:
sen2α = 0,36, extraes raíz cuadrada negativa (recuerda el cuadrante) en ambos miembros, y queda:
senα = -0,6;
luego, planteas la identidad de la cosecante en función del seno, y queda:
cosecα = 1 / senα, reemplazas el valor del seno en el denominador del segundo miembro, y queda:
cosecα = 1 / (-0,6), expresas al denominador en forma fraccionaria, y queda:
cosecα = 1 / (-3/5), resuelves el segundo miembro, y queda:
cosecα = -5/3 ≅ -2,667.
Espero haberte ayudado.