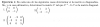En 

de https://matrixcalc.org/es/

te lo hacen paso a paso.

Corresponde a Bachillerato (más bien a 2º)

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

Lo entiendo, muchas gracias de todas formas. ÉXITO SIEMPRE.

Planteas la expresión de la función derivada, y queda:

f ' (x) = 1/x, que evaluada para el estudio queda: f ' (e) = 1/e;

luego, planteas la expresión de la pendiente de la recta normal a la gráfica de la función en el punto de contacto, y queda:

m = -1/f ' (e), reemplazas el valor del denominador, y queda: m = -1/(1/e), resuelves, y queda: m = -e;

luego, con el valor de la pendiente y con las coordenadas del punto de contacto, planteas la ecuación cartesiana de la recta normal, y queda:

y = -e*(x - e) + 2, distribuyes el primer término, y queda:

y = -e*x + e²+2 (1);

luego, planteas la condición de intersección de la recta normal con el eje OX, y queda:

y = 0, sustituyes la expresión señalada (1), y queda:

-e*x + e²+2 = 0, aquí restas (e²+2) en ambos miembros, y queda:

-e*x = -(e²+2), divides por -e en ambos miembros, y queda:

x = (e²+2)/e, distribuyes el denominador, y queda:

x = e+2/e ≅ 3,454,

que es la abscisa del punto de intersección de la recta normal con el eje OX: B(e+2/e,0).

Luego, planteas la condición de intersección de la gráfica de la función con el eje OX, y queda:

f(x) = 0, sustituyes la expresión de la función, y queda:

lnx + 1 = 0, aquí restas 1 en ambos miembros, y queda:

lnx = -1, compones en ambos miembros con la función inversa del logaritmo natural, y queda:

x = e^-1 = 1/e ≅ 0,368,

que es la abscisa del punto de intersección de la gráfica de la función con el eje OX: A(1/e,0).

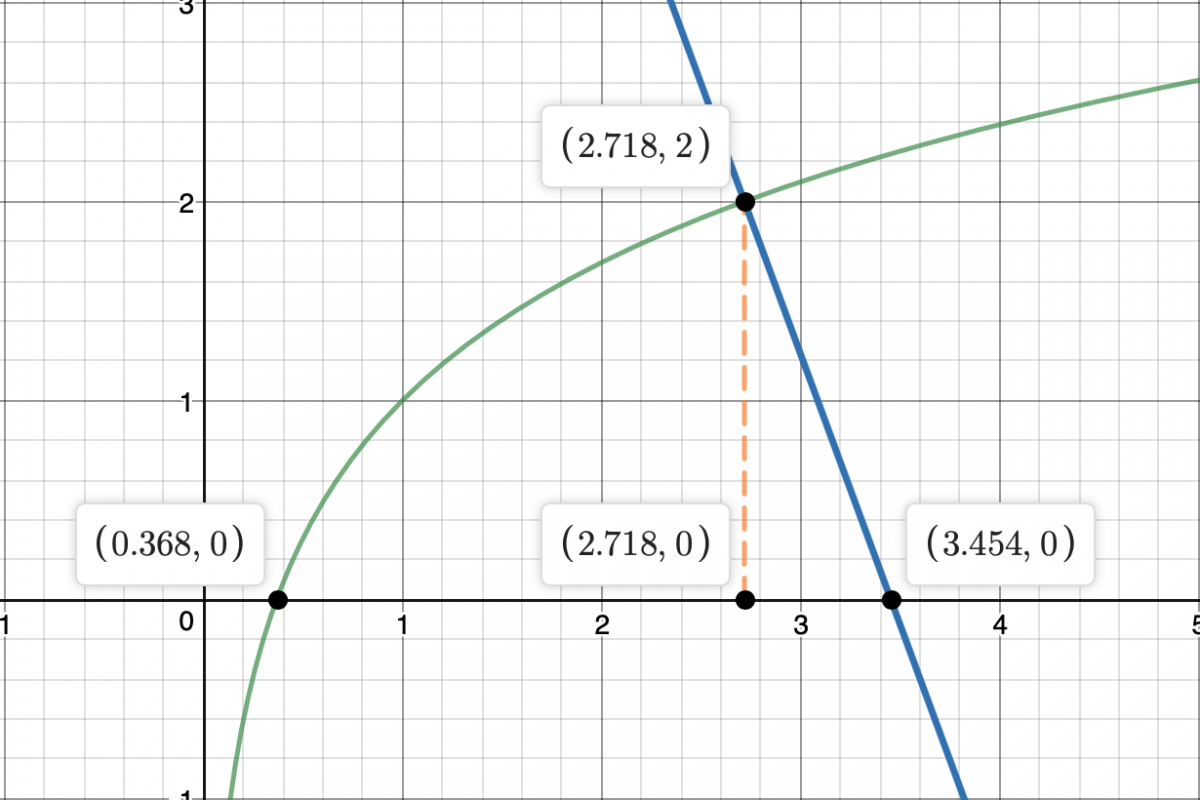
Luego, haz un gráfico, y verás que la región determinada por la gráfica de la función, la recta normal y el eje OX se asemeja a un triángulo con base en el eje OX, cuyos vértices son los puntos: A(1/e,0), P(e,2) y B(e+2/e,0);

luego, trazas la recta paralela a eje OY que pasa por el punto P (x = e), y tienes que la región queda dividida en dos subregiones:

R₁, limitada inferiormente por el eje OX y superiormente por la gráfica de la función;

R₂, limitada inferiormente por el eje OX y superiormente por la recta normal;

luego, planteas que el área total es igual a la suma de las áreas de las dos subregiones, y queda:

A_R = ₀∫^e (lnx + 1)*dx +  _e∫^(e+2/e) (-e*x + e²+2)*dx,

y queda que resuelvas ambas integrales.

Espero haberte ayudado.

lo podemos hacer, como nos sugiere Antonio, a lo largo del eje x:

A = _1/e∫^e (lnx + 1)dx  +  _e∫^e+2/e (-xe + e2+2)dx = 3.0861 + 0.7357 = 3.8219 u²

o a lo largo del eje y:

A = ₀∫² [(e²+2-y)/e-e^y-1]dy = 3.8219 u²

pues:

y = -xe + e2+2 => x = (e²+2-y)/e

y= lnx +1 => x = e^y-1

Yo no se hacerlo, ¿contento?

Está cortado el enunciado. sube foto completa.

Asíntotas