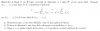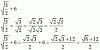-
pooooor faaaas ayudenme con este mañana tengo examen y necesito que me lo resuelvaaaan ahoraaa empieza con esa S Agrande pero nose como hacerla -2x(x^-3)^2dx
Luis Cano
el 11/1/19 -
Buenas tengo esta funcion que esta encerrada con un cuadrado me pide hallar su inversa de esa funcion y solo pude llegar hasta donde se ve en la foto alguien me puede ayudar por favor no puedo despejar y, o alguien que me enseñe de que manera puedo sacar la inversa de esta funcion gracias de antemano.....por si no se llega a notar laparte de abajo es e elevado a x-1 y arriba es e elevado a x+1
Luis Cano
el 11/1/19Antonio Silvio Palmitano
el 11/1/19Tienes la expresión de la función:
f(x) = (ex+1 - 3)/(ex-1 + 6),
y observa que su dominio es:
Df = (-∞,+∞) = R,
ya que su denominador es una suma de dos términos estrictamente positivos.
Luego, puedes plantear la expresión de los elementos de la imagen de la función:
f(x) = y, sustituyes la expresión de la función en el primer miembro, y queda:
(ex+1 - 3)/(ex-1 + 6) = y, multiplicas por (ex-1 + 6) en ambos miembros, y queda:
ex+1 - 3 = y*(ex-1 + 6), distribuyes el segundo miembro, y queda:
ex+1 - 3 = y*ex-1 + 6*y,
aplicas la propiedad de la multiplicación de potencias con bases iguales y de la división de potencias con bases iguales en las expresiones exponenciales, y queda:
ex*e - 3 = y*ex/e + 6*y, multiplicas por e en todos los términos de la ecuación, y queda:
ex*e2 - 3e = y*ex + 6e*y, restas y*ex y sumas 3e en ambos miembros, y queda:
ex*e2 - y*ex = 6e*y + 3e, extraes factores comunes en ambos miembros, y queda:
ex*(e2 - y) = 3e*(2y + 1), divides por (e2 - y) en ambos miembros, y queda:
ex = 3e*(2y + 1) / (e2 - y);
luego, observa que el primer miembro es estrictamente positivo por lo que el segundo miembro también debe serlo, compones en ambos miembros con la función inversa del logaritmo natural, y queda:
x = ln( 3e*(2y + 1) / (e2 - y) ), aplicas la propiedad del logaritmo de una multiplicación, y queda:
x = ln(3) + ln(e) + ln( (2y + 1) / (e2 - y) ), resuelves el segundo término, y queda:
x = ln(3) + 1 + ln( (2y + 1) / (e2 - y) ) (1),
que es la expresión de un elemento del dominio de la función en función de su elemento correspondiente en la imagen,
y observa que tienes dos opciones para el argumento del logaritmo natural:
a)
2y + 1 > 0 y e2 - y > 0, y de aquí despejas:
y > -1/2 y y < e2, que conduce al intervalo:
Ia = (-1/2, e2);
b)
2y + 1 < 0 y e2 - y < 0, y de aquí despejas:
y < -1/2 y y > e2, que son inecuaciones incompatibles, por lo que tienes:
Ib = Φ;
luego, planteas que la imagen de la función es igual a la unión de los dos intervalos, y queda:
If = (-1/2, e2).
Luego, permutas variables en la ecuación señalada (1), y queda:
y = ln(3) + 1 + ln( (2x + 1) / (e2 - x) ),
que es la expresión de la función inversa, por lo que puedes expresarla:
f-1(x) = ln(3) + 1 + ln( (2x + 1) / (e2 - x) ),
cuyo dominio coincide con la imagen de la función de tu enunciado, por lo que queda expresado:
D1 = (-1/2, e2),
y cuya imagen coincide que el dominio de la función de tu enunciado, por lo que queda expresada:
I1 = (-∞,+∞) = R.
Espero haberte ayudado.
-
Alguien me podría ayudar a resolver estos dos sistemas logarítmicos por favor??
a)x-y=9
log x-log y=1
b)log (2x-4)+log y =2
4x-y=-9
Francisco Javier Tinoco Tey
el 10/1/19 -
Porfavor me podriais decir donde puedo encontrar problemas aritmeticos de 2 de la eso
de grifos con desague y sin desague
-
Hola, estaba con este problema de la ABAU
9. Dadas las rectas y a) Estudia la posición relativa de r y s . Calcula la distancia de r a s . b) Se dos lados de un rectángulo están sobre las rectas r y s y dos vértices consecutivos del rectángulo son los puntos A(0,1,1) y B(0,4,4), calcula las coordenadas de los otros dos vértices y el área del rectángulo.
y la verdad es que el apartado b) no sé hacerlo, alguien podría darme indicaciones? Infinitas^(infinitas) gracias :-)
ALOFRE
el 10/1/19 -
Me podéis ayudar con este problema?
Un vendedor compra un número determinado de garrafas de 10litros de aceite por un total de 180€.
El aceite lo envasa en botellas de 2 litros y las vende a 30€ cada una.
¿ Cuantas garrafas ha de comprar para obtener una ganancia de 270€?
Gracias
-
Holaaa! Me podési ayudar con este ejercicio de espacios duales? Tengo dudas con el apartado 3c.
Muchas graciias!!
Antonius Benedictus
el 10/1/19¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).