-
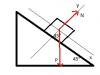
Hola, por problemas inesperados solo tuve una clase de dinámica, tengo este ejercicio propuesto que la verdad no tengo ni idea de como hacerlo. Agradecería ayuda de algún universitario con el planteo del sistema de coordenadas adecuado y los cálculos. El problema se ve en la imagen

Francisco Javier
el 17/2/17Todo el sistema se mueve hacia la izquierda.
Sin fricción:
Análisis de cuerda: 2x1 - x2 = c → 2v1 - v2 = 0 → 2a1 - a2 = 0 → a2 = 2a1 = 2*1.34 ≈ 2.68 m/s2
Para m1: ∑Fx = m1a1 → m1*g*Sin(α) - 2T = m1a1 → 37*9.81*Sin(44.4º) - 2T = 37*1.34 → T ≈ 102.188 N
Para m2: ∑Fx = m2a2 → T - m2*g*Sin(β) = m2a2 → 102.188 - 9.56*9.81*Sin(β) = 9.56*2.68 → β ≈ 54.728º
Con fricción:
Para m1: ∑Fx = m1a1 → m1*g*Sin(α) - 2T - μk*m1*g*Cos(α) = m1a1 → 37*9.81*Sin(44.4º) - 2T - 0.521x10-1*37*9.81*Cos(44.4º) = 37*0.5*a2 (1)
Para m2: ∑Fx = m2a2 → T - m2*g*Sin(β) - μk*m2*g*Cos(β) = m2a2 → T - 9.56*9.81*Sin(54.728º) - 0.521x10-1*9.56*9.81*Cos(54.728º) = 9.56*a2 (2)
Resolviendo sistema 2x2 obtienes que T ≈ 100.142 N y que a2 ≈ 2.171 m/s2
Para que el sistema se mueva a velocidad constante, no debe haber aceleración. Usamos las ecuaciones (1) y (2) pero esta vez igualadas a cero y teniendo como incogninta μk
m1*g*Sin(α) - 2T - μk*m1*g*Cos(α) = 0 → 37*9.81*Sin(44.4º) - 2T - μk*37*9.81*Cos(44.4º) = 0 (3)
T - m2*g*Sin(β) - μk*m2*g*Cos(β) = 0 → T - 9.56*9.81*Sin(54.728º) - μk*9.56*9.81*Cos(54.728º) = 0 (4)
Resolviendo sistema 2x2 obtienes que T ≈ 91.419 N y que μk ≈ 0.274
Tomamos μk = 0.521x10-1. Con este valor hallamos que a2 = 2.171 m/s2. Por Cinemática sabemos que t = (vf - vo) / a. Reemplazando: t = (0 - 4.19) / - 2.171 ≈ 1.93 s
Para ese mismo valor de coeficiente de roce hallamos que a1 = 0.5*a2 = 0.5*2.171 ≈ 1.085 m/s2. Y la distancia que recorre m1 será de: d = 0.5*a*t2 = 0.5*1.085*1.932 ≈ 2.021 m
OJO: Resolví a lo que entendí. El enunciado de preguntas es un desorden total. Malísima la redacción.
-
Hola, necesito algo de ayuda con este ejercicio. Entiendo que se resuelve por consevación de la cantidad de movimiento, pero me confundo al utilizar dos sistemas de refencia y no logro llegar a los resultados esperados. Si alguien me puede ayudar a plantearlo será de mucha ayuda, desde ya muchas gracias.
Francisco Javier
el 17/2/17Cantidad de movimiento (p) es el producto de la masa por la velocidad p = mv
Llamaremos mg a Gilberto, mj a Juan y mc a la caja. Por lo tanto vg, vj y vc serán las velocidades de Gilberto, Juan y la caja respectivamente.
Parte a):
La cantidad de movimiento inicial sería igual a la cantidad de movimiento final. Inicialmente todo esta quieto, por lo tanto la cantidad de movimiento inicial es cero.
Tomando un marco de referencia con respecto al suelo, los jóvenes al saltar tendrán una velocidad igual a la del brinco menos la velocidad de la caja.
Aparte, debes tener en cuenta que cuando ambos jóvenes saltan la caja se moverá en sentido contrario al salto, por lo que la velocidad de la caja debes colocarle signo negativo.
po = pf → 0 = mgvg + mjvj + mcvc → 0 = 45*(4 - vc) + 75*(4 -vc) + 15*(-vc) → vc ≈ 3.556 m/s
Parte b):
Se conserva la cantidad de movimiento. La cantidad de movimiento inicial sigue siendo cero. Deberemos calcular primero una velocidad de caja v' producto del salto solo de Juan.
po = pf → 0 = mjvj + (mg + mc)v' → 0 = 75*(4 - v') + (45 + 15)(-v') → v' ≈ 2.222 m/s
Cuando luego salta Gilberto, ya la cantidad de movimiento inicial no será cero. Esta tendra un valor.
po = pf → (mg + mc)(-v') = mgvg + mcvc → (45 + 15)(-2.222) = 45*(4 - vc) + 15*(-vc) → vc ≈ 5.222 m/s
Parte c):
Mismo procedimiento que b). Calculamos primero la velocidad v' que proporciona solo Gilberto:
po = pf → 0 = mgvg + (mj + mc)v' → 0 = 45*(4 - v') + (75 + 15)(-v') → v' ≈ 1.333 m/s
Y despues cuando salta Juan:
po = pf → (mj + mc)(-v') = mjvj + mcvc → (75 + 15)(-1.333) = 75*(4 - vc) + 15*(-vc) → vc ≈ 4.667 m/s
-
Hola, necesito ayuda con un ejercicio de mi sobrino que va a 4 de la ESO:
Sobre un cuerpo de m=15kg, que se mueve sobre una superficie horizontal de u=2, actúa una fuerza F=200N. Calcula:
a) El trabajo de la fuerza resultante.b) el incremento de energía cinética y la velocidad final del cuerpo.
Si alguien me puede ayudar se lo agradecería muchísimo.
Gracias!
Antonio Silvio Palmitano
el 17/2/17 -
hola Unicoos, voy a necesitar un poco de su sabiduría aquí. Quería saber porque el producto de Uo* |H| (excitación magnética) es igual al campo en el vacío, si bien dice que es lo mismo en el vacío o en el material no logro comprender si ese es el motivo o hay algo más. Gracias!

David
el 20/2/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
Jose
el 20/2/17David, ya encontre el porque y les dejo la respuesta para algún futuro..
El producto ese es el campo magnetico en el vacío ya que nosotros en primera instancia sabemos que el campo en el material es : B= Uo* H + Uo*M. Donde la magnetización tiene que ver con el material del conductor, al suponerla uniforme M=0. Entonces solo nos queda que el campo sería B=Uo * H. Lo cual equivale a las corrientes libres del vacío
-
Buenas!
Tengo un problema el cual no consigo resolver... Me pide que calcule el peso de un cuerpo sobre el que actúa una fuerza normal de 35N cuando está apoyado sobre una superficie de 45º con respecto a la horizontal. ¿Como hallo el peso si no me especifica la masa?
Antonio Silvio Palmitano
el 16/2/17Observa que el ángulo de inclinación del plano con respecto a la horizontal tiene la misma medida del ángulo que forman el peso con la recta perpendicular al plano.
Definimos un sistema de referencia con origen de coordenadas en el centro de masa del cuerpo, eje OX paralelo al plano y eje OY perpendicular al plano.
Luego, descomponemos al peso según los ejes OX y OY y tenemos:
Px = P*sen45°
Py = P*cos45°
Luego, planteamos la condición de equilibrio para el eje OY, al que consideramos positivo hacia arriba;
N - Py = 0, hacemos pasaje de término y queda:
- Py = - N, multiplicamos en ambos miembros por -1 y queda:
Py = N, sustituimos la expresión de la componente del peso y queda:
P*cos45° = N, hacemos pasaje de factor como divisor, reemplazamos el valor de N y queda:
P = 35/cos45°, resolvemos y queda:
P ≅ 49,497 (en N).
Espero haberte ayudado.
-
Jesus Diaz Castro
el 16/2/17Son cálculos bastante fáciles, así que te los voy a dejar a ti.
El trabajo W = F·Δx
Sabes que la masa del cuerpo son 2 Kg y que F=ma y la aceleración de ese sistema estoy segurísimo de que sabes deducirla tu sola.
Bien ya tienes el peso P, ahora viene lo más "difícil", a partir del centro de gravedad del cuerpo tienes que establecer el eje de coordenadas para sacar las componentes de las fuerzas.
Donde te quedarán Pcos30 y Psen30.
Bien si consideramos que NO hay rozamiento tan solo calcula W con Pcos30
Cuando SÍ lo consideres ten en cuenta que N = Psen30 y que Fr = N·μ y este valor de W (llamémosle W2 ) lo tienes que sumar con el valor de W obtenido en el apartado anterior (W1) para obtener WT
Espero haberte ayudado Laura
-
Antonio Silvio Palmitano
el 16/2/17Planteamos:
a = kx - ωt (1), luego la ecuación de la primera onda queda: y1 = A*sen(a);
b = kx - ωt + δ (2), luego la ecuación de la segunda onda queda: y2 = A*sen(b).
Luego, por el principio de superposición tienes planteado:
y = y1 + y2, sustituimos expresiones y queda:
y = A*sen(a) + A*sen(b), extraemos factor común y queda:
y = A*( sen(a) + sen(b) ), luego aplicamos la identidad trigonométrica del enunciado y queda:
y = A*2*sen( (a+b)/2 )*cos( (a-b)/2 ) (3).
Luego, a partir de las expresiones señaladas (1) (2) tenemos:
(a + b)/2 = sustituimos = (kx - ωt + kx - ωt + δ)/2 = (2kx - 2ωt + δ)/2 = distribuimos el denominador = (kx - ωt + δ/2) (4);
(a - b)/2 = sustituimos = (kx - ωt - kx + ωt - δ)/2 = cancelamos términos opuestos = (-δ/2) (5).
Luego, sustituimos las expresiones señaladas (4) (5) en la ecuación señalada (3) y queda:
y = 2A*sen(kx - ωt + δ/2)*cos(-δ/2), aplicamos la identidad trigonométrica del coseno del opuesto de un ángulo y queda:
y = 2A*sen(kx - ωt + δ/2)*cos(δ/2), ordenamos factores y queda:
y = 2A*cos(δ/2)*sen(kx - ωt + δ/2).
Espero haberte ayudado.
-
Buenas.
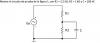
Se que probablemente se salga de los contenidos de unicoos; no obtante, agradecería enormente algo de ayuda con esto, si aguien puediese decirme el valor de la intensidad, y la caída de tensión en cada componente, y como calcularlo. En la foto no se ve, la fuente es de 12V y 5kHz
Muchas gracias.
-
Buenos dias , podriais ayudarme con este ejercicio?
- (2,5 puntos). Supón que vas circulando con tu coche (1 040 kg el coche, más 60 kg de tu persona), y, por un despiste, quedas atascado en el barro de la cuneta. Dos personas que pasaban por allí te ayudan a salir del apuro. Enganchan dos cuerdas en el mismo punto del parachoques, y tiran de él horizontalmente formando las cuerdas entre sí un ángulo de 90º. Cada persona ejerce una fuerza de 800 N.
- Haz un esquema y dibuja todas las fuerzas que actúan sobre el coche al ser arrastrado, representándolas como en la figura adjunta: (0,5 puntos)
- Calcula la fuerza total que hacen sobre el coche las dos cuerdas y la fuerza normal que el suelo realiza sobre él. (Recuerda que las fuerzas son vectores y se suman como tales). (0,5 puntos)
- Pasado el apuro, te subes al coche y le pones en marcha. El coche arranca y en 10 s alcanza una velocidad de 100 km/h. Calcula la aceleración del coche. (0,25 puntos)
- A partir de ahí mantienes la velocidad de 100 km/h. Suponiendo un coeficiente dinámico de rozamiento de 0,2, calcula cuánto vale la fuerza que el motor debe realizar para mantener esa velocidad constante.(0,5 puntos)
- Sigues conduciendo y de pronto ves un obstáculo a 200 m y frenas para quedar detenido justo a esa distancia. ¿Qué le ocurre a un paquete que llevas suelto en el asiento trasero? ¿A qué se debe? ¿Cuánto vale la aceleración de frenado? (0,75 puntos)
-
Hola me podrian explicar :
Cuando la energía potencial aumenta y disminuyeFacu Imfeld
el 16/2/17Cuando lanzas por ejemplo una piedra hacia arriba, la piedra parte de tu mano con una velocidad inicial, es decir que posee cierta energía cinética, pero no posee energía potencial porque estás a nivel del suelo, y a nivel del suelo la altura es 0. Ahora, a medida que la piedra va subiendo, va ganando altura, y su velocidad va disminuyendo, es decir; la energía cinética de la piedra va disminuyendo porque la velocidad de la piedra disminuye, a su vez, la piedra va ganando energía potencial porque va tomando cada vez más altura, hasta llegar a un punto que es su altura máxima, allí, la velocidad de la piedra es 0 y la energía que tiene la piedra es toda potencial. En resumen
Considera primero las dos fórmulas de la energía
Ec = (1/2)mv^2
Ep = mgh
Cuando la piedra parte de tu mano, no hay altura (h=0), la energía de la piedra es toda cinética porque parte con una velocidad
A medida que la piedra va subiendo, su velocidad va disminuyendo y su energía cinética también, proporcionalmente a la disminución de la e cinética, va en aumento la energía potencial.
En la altura máxima, la velocidad de la piedra es 0, es decir que no hay e cinética allí arriba, como la piedra está a una cierta altura, la energía que posee la piedra es toda potencial.
Cualquier duda me la escribes aquí