-
Jon Aginaga
el 14/2/17Si en el campo gravitatorio tengo un problema de energías, ¿cómo sé cómo plantearlos? es decir, si por ejemplo tengo que poner un satélite orbitando a "x" distancia, o si tengo que mandarlo al infinito, ¿cómo diferencio cada situación y planteo la fórmula de la conservación de energías con Ep, Ec y Em? Muchísimas gracias.
Francisco Javier
el 15/2/17Desde la primaria nos enseñaron que la energía mecánica (E) es la suma de la energía cinética (K) más la potencial (U).
También a estas alturas debes saber que K = 0.5mv2 (sin relevancia para la ocasión) y que U = - GmM/r
En el estudio del movimiento planetario se demostró que la energía mecánica de un satélite en órbita viene dado por E = - GmM/2r
Si aplicamos conservación de energía entre la superficie de la Tierra y el punto de orbita nos queda esto: K - GmMT/RT = - GmMT/2r
Despejando para K: K = GmMT/r - GmMT/2r = GmMT[(1/RT)-(1/2r)]. Esta sería la energía para poner el satélite a una distancia r del planeta.
Ahora si queremos mandar el satélite al infinito, pues solo en la expresión anterior sustituimos r = inf. Si hacemos esto 1/2r = 1/2(inf) = 0. Y la expresión quedaría:
K = GmMT/RT. Esta sería la energía para mandar el satélite al infinito.
Jon Aginaga
el 15/2/17Muchas gracias! Una última duda, cuando decías
K = GmMT/r - GmMT/2r = GmMT[(1/RT)-(1/2r)].
Que era una energía para ponerla en órbita, se refiere a que pone el satélite girando en la órbita, o simplemente llevarlo? Es decir, hay una fórmula para dejarlo sin que orbite (simplemente llevarlo), y otra que orbite. ¿Qué fórmula tiene cada una? De verdad, muchas gracias.
-
Jon Aginaga
el 14/2/17¿Cuáles son las fórmulas que tengo que saber para poder hacer cualquier ejercicio de campo elétrico?
-
José
el 14/2/17Sobre un cuerpo de 5 kg actúa una fuerza. El coeficiente de rozamiento entre la superficie y el cuerpo es de 0,3. Encuentra la aceleración del sistema para cada caso:
a) La fuerza es de 30 N y hace un ángulo con la horizontal de 30º hacia arriba.
b) La fuerza es de 30 N pero el ángulo con la horizontal se 30º pero hacia abajo.
-
Adrián López
el 14/2/17
-
Samantha Ortega
el 14/2/17Hola no se como resolver este ejercicio serian tan amables de ayudarme
El cuerpo A de masas 10kg viene con velocidad 20 m/s y choca al cuerpo B de masa 5kg que inicialmente se encuentra detenido. Los cuerpos chocan y rebotan. Calcular las velocidades de cada cuerpo después de la colisión. Suponiendo que no se pierde energía en el choque
Muchas gracias...
Antonio Silvio Palmitano
el 14/2/17Tienes que el choque es perfectamente elástico, por lo que debes plantear conservación de la energía cinética, además de conservación de la cantidad de movimiento como todo choque donde no actúan fuerzas de rozamiento.
Tienes antes del choque:
ECa = (1/2)*10*202 + (1/2)*5*02 = 2000 + 0 = 2000 (en J);
pa = 10*20 + 5*0 = 200 + 0 = 200 (en Kg*m).
Tienes después del choque:
ECd = (1/2)*10*v12 + (1/2)*5*v22 = 5*v12 + 2,5*v22 (en J);
pd = 10*v1 + 5*v2 (en Kg*m).
Luego, planteamos las conservaciones de la energía cinética y de la cantidad de movimiento y queda el sistema:
ECa = ECd
pa = pd
sustituimos expresiones y queda:
2000 = 5*v12 + 2,5*v22
200 = 10*v1 + 5*v2
dividimos en todos los términos de la primera ecuación por 2,5, dividimos por 5 en todos los términos de la segunda ecuación por 5 y queda:
800 = 2*v12 + v22
40 = 2*v1 + v2
y queda para que resuelvas el sistema de ecuaciones (observa que v1 debe tener signo negativo, y v2 signo positivo, ya que hemos considerada como positivo al sentido de la velocidad del primer cuerpo antes del choque).
Espero haberte ayudado.
-
Angel
el 14/2/17 -
Marco
el 13/2/17Tengo una duda con este problema, a mi me da 6,83 pero mi hora de respuestas dice que da 13,7 rad/s. Alguien puede ayudarme a saber cual es la correcta?
Una rueda rotatoria requiere 3 s para girar 37 rev. Su velocidad angular al final del intervalo de 3 s es 98 rad/s ¿Cuál es la aceleración angular, constante, de la rueda?
Antonio Silvio Palmitano
el 14/2/17Planteamos que la posición angular inicial es cero y planteamos las ecuaciones:
θ = ω0*t + (1/2)*α*t2
ω = ω0 + α*t
Luego, tenemos los datos: t = 3 (en s), θ = 37*2π = 74π (en rad), ω = 98 (en rad/s), reemplazamos y queda el sistema:
74π = ω0*3 + (1/2)*α*9
98 = ω0 + α*3
resolvemos factores numéricos, ordenamos factores en los términos de ambas ecuaciones y queda:
74π = 3*ω0 + (9/2)*α
98 = ω0 + 3*α, de aquí despejamos: 98 - 3*α = ω0 (1),
luego sustituimos en la primera ecuación y queda:
74π = 3*(98 - 3*α) + (9/2)*α, distribuimos y queda:
74π = 294 - 9*α + (9/2)*α, hacemos pasaje de término, reducimos términos semejantes y queda:
- 61,52 = - (9/2)*α, , hacemos pasaje de factor como divisor y queda:
13,67 = α (en rad/s2),
luego reemplazamos en la ecuación señalada (1) y queda:
98 - 3*13,67 = ω0, resolvemos y queda:
58,98 = ω0 (en rad/s).
Espero haberte ayudado.
-
Jon Aginaga
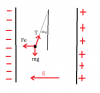
el 13/2/17Me plantean este problema; una esfera de 0.2 gramos se columpia por un hilo de masa despreciable. Su carga es de 6.10^(-9)C, y se encuentra entre dos placas paralelas que se distancian 5 centímetros el uno del otro. El hilo forma 30 grados con la vertical. ¿Cuál es la intensidad del campo eléctrico entre las placas? No soy capaz de hacerlo, ya que no consigo despejar la tensión, pese haberlo intentado diversas veces. Muchas gracias de antemano.
Francisco Javier
el 14/2/17 -
Enrique Sánchez Sancho
el 13/2/17¿Qué fórmulas tengo que saberme para el tema de campo magnético?
Facu Imfeld
el 14/2/17F = q v B (Fuerza Magnética en una partícula)
(q) Carga
(B) Campo magnético
(v) producto vectorial
F = u0I1I2 / 2pi.r (Fuerza Magnética entre conductores paralelos)
u0 (constante magnética)
I1 (intensidad del conductor 1)
I2 (intensidad del conductor 2)
r (distancia a la que se encuentran)
E = B.A.cos(&)
(E) Fem inducida
(B) Campo magnético
(A) Vector área
cos(&) Ángulo que forman los vectores área y campo
B = (u0/4pi).I/r^2 Fórmula de Biot Savart
-
Enrique Sánchez Sancho
el 13/2/17Por un conductro rectilíneo e indefinido circula uan corriente eléctrica de intensidad I = 2 A. S e sitúa una espira cuadrada de lado L = 4 cm a una distancia d = 10 cm tal y como indica la figura. Si por la espira circula una corriente I´ = 3 A en el sentido indicado , calcula la fuerza F (módulo, dirección y sentido) que ejerce la corriente I sobre el lado de la espira más próximo al conductor rectilíneo.
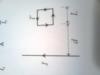
Francisco Javier
el 14/2/17Campo Magnético que se produce en la cara más cerca de la espira por efecto del conductor: B = μo*I / 2*pi*d = 4*pi*1x10-7*2 / [2*pi*10*(1/100)] ≈ 4x10-6 T
Por medio de la regla de la mano derecha (apuntas con el pulgar el sentido de la corriente y la desdobles de los demás dedos te indican el sentido del campo) te das cuenta que dicho campo apunta hacia eje -z.
Teniendo este campo, podemos saber la fuerza en esta parte de la espira aplicando F = I' L B
Reemplazando: F = 3*4*(1/100)*4x10-6 ≈ 4.8x10-7 N
Aplicando nuevamente la regla de la mano derecha (esta vez apuntando con el dedo índice la dirección de la corriente, con el dedo corazón la dirección del campo magnético y el pulgar te dará la dirección de la fuerza) te darás cuenta que dicha fuerza apunta hacia el eje +x.
