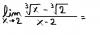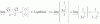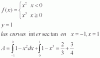Muchas gracias. Pero habrá alguna otra manera de hacerlo sin utilizar L´hopital? es que todavía no me lo enseñaron. O quizá la profe no se dio cuenta... 

Sin L'Hôpital:

Uff... Muchisimas gracias!!! :D

Gracias . El estudio completo lo sabrias hacer? por favor.

Estudio completo de una funcion racional

Sumas y restas 9 en el numerador de la expresión de la función, y queda:

f(x) = ( x²-9 + 4+9 )/(x²-9) = ( (x²-9) + 13 )/(x²-9), distribuyes el denominador, y queda:

f(x) = 1 + 13/(x²-9) (1).

Luego, planteas las expresiones de las derivadas primera y segunda, y quedan:

f ' (x) = -26x/(x²-9)² (2),

f ' ' (x) = 78(x²+3)/(x²-9)³ (3).

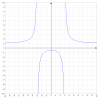
1°)

Dominio: D = (-∞,-3) ∪ (-3,3) ∪ (3,+∞).

Asíntotas horizontales:

Lím(x→±∞) f(x) = Lím(x→±∞) ( 1 + 13/(x²-9) ) = 1,

por lo que la recta cuya ecuación es: y = 1 es asíntota horizontal izquierda y derecha de la gráfica de la función.

Asíntotas verticales:

Lím(x→-3-) f(x) = Lím(x→-3-) ( 1 + 13/(x²-9) ) = +∞,

Lím(x→-3+) f(x) = Lím(x→-3+) ( 1 + 13/(x²-9) ) = -∞,

por lo que la recta cuya ecuación es: x = -3 es asíntota vertical superior por izquierda e inferior por derecha;

Lím(x→3-) f(x) = Lím(x→3-) ( 1 + 13/(x²-9) ) = -∞,

Lím(x→3+) f(x) = Lím(x→3+) ( 1 + 13/(x²-9) ) = +∞,

por lo que la recta cuya ecuación es: x = 3 es asíntota vertical inferior por izquierda y superior por derecha.

2°)

Valores críticos:

f ' (x) = 0, sustituyes la expresión señalada (2), y queda:

-26x/(x²-9)² = 0, multiplicas en ambos miembros por -(x²-9)²/26, y queda: 

x = 0,

luego, evalúas la expresión de la derivada segunda para el valor remarcado, y queda:

f ' ' (0) = 234/(-729) = -26/81 < 0, por lo que tienes que la gráfica de la función es cóncava hacia abajo para el valor crítico,

por lo que tienes que la gráfica de la función presenta un máximo local para x = 0, y el valor de la función para él es:

f(0) = 1 + 13/(-9) = 1 - 13/9 = -4/9.

3°)

Posibles inflexiones:

f ' ' (x) = 0, sustituyes la expresión señalada (3), y queda:

78(x²+3)/(x²-9)³ = 0, multiplicas en ambos miembros por (x²-9)³/78, y queda:

x² + 3 = 0, que es una ecuación polinómica cuadrática que no tiene soluciones reales,

por lo que tienes que la gráfica de la función no presenta puntos de inflexión.

4°)

Crecimiento:

f ' (x) > 0, sustituyes la expresión señalada (2), y queda:

-26x/(x²-9)² > 0, multiplicas por -(x²-9)²/26 (observa que cambia la desigualdad, y queda:

x < 0, por lo que tienes que la gráfica de la función es creciente en el intervalo: (-∞,-3) ∪ (3,0).

Decrecimiento:

f ' (x) < 0, sustituyes la expresión señalada (2), y queda:

-26x/(x²-9)² < 0, multiplicas por -(x²-9)²/26 (observa que cambia la desigualdad, y queda:

x > 0, por lo que tienes que la gráfica de la función es creciente en el intervalo: (0,3) ∪ (3,+∞).

5°)

Concavidad hacia arriba:

f ' ' (x) > 0, sustituyes la expresión señalada (3), y queda:

78(x²+3)/(x²-9)³  > 0, divides en ambos miembros por 78(x²+3) (observa que no cambia la desigualdad), y queda:

1/(x²-9)³  > 0, extraes raíz cúbica en ambos miembros (observa que no cambia la desigualdad), y queda:

1/(x²-9) > 0, factorizas el denominador del primer miembro, y queda:

1 / (x+3)(x-3) > 0, y observa que la inecuación es válida cuando los dos factores del denominador tienen signos iguales,

por lo que tienes que la gráfica de la función es cóncava hacia arriba en el intervalo: (-∞,-3) ∪ (3,+∞).

Concavidad hacia abajo:

f ' ' (x) < 0, sustituyes la expresión señalada (3), y queda:

78(x²+3)/(x²-9)³  < 0, divides en ambos miembros por 78(x²+3) (observa que no cambia la desigualdad), y queda:

1/(x²-9)³  < 0, extraes raíz cúbica en ambos miembros (observa que no cambia la desigualdad), y queda:

1/(x²-9) < 0, factorizas el denominador del primer miembro, y queda:

1 / (x+3)(x-3) < 0, y observa que la inecuación es válida cuando los dos factores del denominador tienen signos distintos,

por lo que tienes que la gráfica de la función es cóncava hacia abajo en el intervalo: (-3,3).

Espero haberte ayudado.

Haz un gráfico, y verás que tienes dos subregiones:

R₁:

limitada superiormente por la recta cuya ecuación es y = 1, inferiormente por la curva cuya ecuación es y = x²,

y por derecha por el eje coordenado OY, y observa que la región tiene forma parecida a un triángulo, y sus vértices son: (-1,1), (0,0) y (0,1);

luego, su planteas su área:

A₁ = _-1∫⁰ (1 - x²)*dx = [x - x³/3] = evalúas = (0 - 0) - (-1 + 1/3) = 2/3;

R₂:

limitada superiormente por la recta cuya ecuación es y = 1, inferiormente por la curva cuya ecuación es y = x³,

y por derecha por el eje coordenado OY, y observa que la región tiene forma parecida a un triángulo, y sus vértices son: (0,0), (1,1) y (0,1);

luego, su planteas su área:

A₂ = ₀∫¹ (1 - x³)*dx = [x - x⁴/4] = evalúas = (1 - 1/4) - (0 - 0) = 3/4.

Luego, puedes plantear que el área de la región es igual a la suma de las áreas de las subregiones, y queda:

A_R = A₁ + A₂ = 2/3 + 3/4 = 17/12.

Espero haberte ayudado.

Foto del enunciado original, por favor.

Logaritmos    secundaria

https://www.matematicasonline.es/cuarto-eso/ejercicios/Logaritmos.pdf

https://www.matematicasonline.es/cuarto-eso/ejercicios/Logaritmos2.pdf

Esa gramática Antonia , un pelín mejor.

OJo:  si  log(A^2)=2*log(abs(A))

3)

log₆( (5x-9)² ) = 4,

observa que el argumento del logaritmo es positivo para todo número real distinto de 9/5,

por lo que al aplicar la propiedad del logaritmo de una potencia debes tener en cuenta el valor absoluto de su base, luego queda:

2*log₆( |5x-9| ) = 4, divides por 2 en ambos miembros, y queda:

log₆( |5x-9| ) = 2,

compones en ambos miembros con la función inversa del logaritmo en base 6, y queda:

|5x - 9| = 36,

luego, por definición de valor absoluto, tienes dos opciones:

a)

5x -9 = -36, sumas 9 en ambos miembros, luego divides por 5 en ambos miembros, y queda:

x = -27/5;

b)

5x -9 = 36, sumas 9 en ambos miembros, luego divides por 5 en ambos miembros, y queda:

x = 9.

5)

log( √(x²+64) ) = 1, aplicas la propiedad del logaritmo de una raíz, y queda:

(1/2)*log(x²+64) = 1, multiplicas por 2 en ambos miembros, y queda:

log(x²+64) = 2, compones en ambos miembros con la función inversa del logaritmo decimal, y queda:

x² + 64 = 100, restas 64 en ambos miembros, y queda:

x² = 36, extraes raíz cuadrada en ambos miembros, y tienes dos opciones:

a)

x = -6;

b)

x = 6.

Espero haberte ayudado.

E

https://www.youtube.com/watch?v=Z0XSi3oaicc

Ojalá te ayude