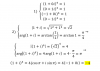Puedes plantear la expresión de la función:

f(x,y) = 36y² + 9x (1), que es la que debemos minimizar.

Luego, tienes la ecuación de restricción:

(x+10)(y-7) = 5488, divides por y-7 en ambos miembros, luego restas 10 en ambos miembros, y queda:

x = 5488/(y-7) - 10 (2).

Luego, sustituyes la expresión señalada (2) en la expresión de la función señalada (1), y queda:

f(y) = 36y² + 9( 5488/(y-7) - 10 ),

distribuyes el último término, y queda:

f(y) = 36y² + 49392/(y-7) - 90 (3),

que es la expresión de la función reducida a una sola variable.

Luego, planteas la expresión de la función derivada, y queda:

f ' (y) = 72y - 49392/(y-7)² (*);

luego, planteas la condición de valor crítico (posible máximo o posible mínimo):

f ' (y) = 0, sustituyes la expresión de la función derivada en el primer miembro, y queda:

72y - 49392/(y-7)² = 0, divides por 72 en ambos miembros, y queda:

y - 686/(y-7)² = 0, sumas 686/(y-7)² en ambos miembros, y queda:

y = 686/(y-7)², multiplicas por (y-7)² en ambos miembros, y queda

y*(y-7)² = 686,

que es una ecuación polinómica cúbica, y observa que una de sus soluciones es: y = 14.

Luego, desarrollas el primer miembro de la ecuación, restas 686 en ambos miembros, y queda:

y³ - 14y² + 49y - 686 = 0;

luego, factorizas el primer miembro (observa que puedes dividir por (y-14) mediante la Regla de Ruffini), y la ecuación queda:

(y-14)*(y²+49) = 0,

y observa que el segundo factor no tiene raíces reales, por lo que tienes que el único valor crítico de la función es: y = 14.

Luego, derivas la expresión de la función derivada primera señalada (*), y queda:

f ' ' (y) = 72 + 98784/(y-7)³,

y observa que toma un valor positivo para y = 14, por lo que puedes concluir que la función presenta un mínimo para dicho valor crítico, ya que la gráfica de la función es cóncava hacia arriba para él.

Luego, reemplazas el valor crítico (y = 14) en la ecuación señalada (2), y queda:

x = 5488/(14-7) - 10 = 784 - 10 = 774.

Luego, tienes que los valores que cumplen con las condiciones del enunciado son:

x = 774, y = 14.

Espero haberte ayudado.

1)

Puedes plantear la ecuación:

w⁴ = 1, extraes raíz cuadrada en ambos miembros, y tienes dos opciones:

a)

w² = 1, aquí extraes raíz cuadrada en ambos miembros, y queda: w₁ = -1 y w₂ = 1;

b)

w² = -1, aquí extraes raíz cuadrada en ambos miembros, y queda: w₃ = -i y w₄ = i.

2)

Tienes la expresión:

(1 + i)⁴ = ( (1 + i)² )² = desarrollas el binomio elevado al cuadrado, y queda:

= ( 1 + 2i - 1 )² = cancelas términos opuestos en el argumento de la potencia, y queda:

= ( 2i )² = distribuyes el exponente, y queda:

= 4i² = resuelves el segundo factor, y queda:

= 4(-1) = -4.

Espero haberte ayudado.

Suponemos que los rebotes de la pelota en los bordes del cuadrado son perfectos.

Puedes llamar A(0,1) al punto de partida,

puedes llamar B(b,4) al punto de rebote en el lado superior del cuadrado,

puedes llamar C(c,0) al punto de rebote en el lado inferior del cuadrado,

y puedes llamar D(4,2) al último punto.

Luego, tienes para la pendiente del primer segmento: m_AB = (b-0)/(4-1) = b/3.

Luego, tienes para la pendiente del segundo segmento: m_BC = (c-b)/(0-4) = -(c-b)/4.

Luego, tienes para la pendiente del tercer segmento: m_CD = (4-c)/(2-0) = (4-c)/2.

Luego, observa en tu dibujo que la pendiente del primer segmento es igual a la pendiente del tercero, y observa que la pendiente del primer segmento es opuesta a la del segundo segmento, por lo que puedes plantear las ecuaciones:

m_AB = m_CD,

m_AB = -m_BC;

luego, sustituyes expresiones, y queda:

b/3 = (4-c)/2,

b/3 = (c-b)/4;

luego, multiplicas por 6 en ambos miembros de la primera ecuación, y multiplicas por 12 en ambos miembros de la segunda ecuación, y queda:

2b = 3(4-c),

4b = 3(c-b),

distribuyes en los segundos miembros, y queda:

2b = 12 - 3c (1),

4b = 3c - 3b (2),

sumas 3b en ambos miembros de la ecuación señalada (2), y queda:

7b = 3c, aquí divides por 7 en ambos miembros, y queda: b = (3/7)c (3);

luego, sustituyes la expresión señalada (3) en la ecuación señalada (1), y queda:

(6/7)c = 12 - 3c, sumas 3c en ambos miembros, y queda:

(27/7)c = 12, multiplicas por 7/27 en ambos miembros, y queda: c = 28/9;

luego, reemplazas el valor remarcado en la ecuación señalada (3), y queda: b = 4/3.

Luego, tienes que los puntos de rebote quedan expresados: B(4/3,4) y C(28/9,0).

Espero haberte ayudado.

¿Cúanto mide el lado del cuadrado?

No podemos ver el cuadrado de la figura. 

Saludos.

Tienes la ecuación implícita que define a y como función de x:

e^y = x,

compones en ambos miembros con la función inversa de la función exponencial natural, y la expresión de la función queda:

y = f(x) = lnx,

derivas con respecto a x, y la expresión de la función derivada primera queda:

y ' = f ' (x) = 1/x,

derivas nuevamente con respecto a x, y la expresión de la función derivada segunda queda:

y ' ' = f ' ' (x) = -1/x².

Espero haberte ayudado.

Restas x y restas 8 en ambos miembros de la ecuación de la recta que tienes en tu enunciado, y queda:

3y = -x - 8, multiplicas por 1/3 en todos los términos de la ecuación, y queda:

y = -(1/3)x - 8/3, que es la ecuación cartesiana explícita de la recta, cuya pendiente es: m = -1/3.

Luego, planteas la expresión de la derivada primera de la función, y queda:

f ' (x) = 2x + 2k, evalúas para el punto en estudio, cuya abscisa es x = -1, y queda:

f ' (-1) = -2 + 2k;

luego, planteas la condición de paralelismo entre la recta tangente y la recta dato, y queda:

f ' (-1) = m, sustituyes expresiones, y queda:

-2 + 2k = -1/3, sumas 2 en ambos miembros, y queda:

2k = 5/3, multiplicas por 1/2 en ambos miembros, y queda: k = 5/6;

luego, reemplazas el valor remarcado en la expresión de la función, y queda:

f(x) = x² + (5/3)x + 5, y la expresión de la función derivada queda:

f ' (x) = 2x + 5/3, y observa que se cumple la condición de paralelismo entre la recta tangente y la recta dato que tienes en tu enunciado.

Espero haberte ayudado.

http://www.jorge-fernandez.es/proyectos/angulo/temas/temab/index.html

Si las rectas dadas son concurrentes (se cortan), está bien.

Aqui lo tienes resuelto por David

Como parece que las rectas se cruzan:

Recta que pasa por un punto y corta otras dos rectas

Con otro método Variación de la constante

factor   integrante      µ=(x-3)  y como exacta.

Integrales inmediatas