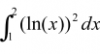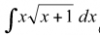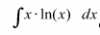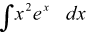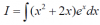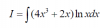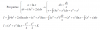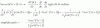-
Mario Perales
el 28/10/17Prueba la integración por partes. Toma como u=( Ln(x) )^2 y como dv = dx. La integral que te salga tras hacer la integral por partes te quedará una con Ln(x), pero sin potencia, por lo que podrás aplicar integración por partes de nuevo. La integral que quedará será ya inmediata.
Un saludo.
Antonio Silvio Palmitano
el 28/10/17Puedes aplicar el Método de Integración por Partes, y observa que deberás hacerlo en dos pasos:
u = (lnx)2, de donde tienes: du = 2(lnx)*(1/x)*dx,
dv = dx, de donde tienes: v = x;
luego aplicas el método, y la integral queda:
I = (lnx)2*x - ∫ x*2(lnx)*(1/x)*dx = (lnx)2*x - 2*∫ lnx*dx,
luego, vuelves a plantear el método: para resolver la integral secundaria:
u = lnx, de donde tienes: du = (1/x)*dx,
dv = dx, de donde tienes: v = x;
luego, aplicas el método, y la integral queda
I = (lnx)2*x - 2*( x*lnx - ∫ x*(1/x)*dx ) = (lnx)2*x - 2*( x*lnx - x),
y solo queda que evalúes la expresión con Regla de Barrow entre 1 y 2.
Espero haberte ayudado.
-
-
Antonio Silvio Palmitano
el 28/10/17Plantea la sustitución (cambio de variable):
x = w2 + 1, de donde tienes: dx = 2w*dw;
luego sustituyes, y la integral queda:
I = ∫ (w2 + 1)*√(w2 + 1 - 1)*2w*dw = ∫ (w2 + 1)*√(w2)*2w*dw = 2*∫ (w2 + 1)*w2*dw = 2*∫ (w4 + w2)*dw,
y puedes continuar la tarea.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 28/10/17Vamos con una orientación.
Los dos ejercicios puedes resolverlos con el Método de Integración por Partes, el primero en un paso, y el segundo en dos pasos:
1)
Plantea:
u = lnx, luego tienes: du = (1/x)*dx; dv = x*dx, luego tienes: v = x2/2, y puedes continuar la tarea.
2)
Plantea:
u = x2, luego tienes: du = 2*x*dx; dv = ex*dx, luego tienes: v = ex, y puedes continuar la tarea,
y verás que la integral secundaria también se podrás resolverla con el mismo método.
Espero haberte ayudado.
-
Ayuda, La suma de las raíces de un ecuación de segundo grado que tiene por coeficiente del termino cuadrático la unidad, por coeficiente del termino lineal una de sus raíces y por termino independiente la otra raíz, es el inverso ...
a) aditivo de -2 b) multiplicativo de 2 c) multiplicativo 1
d) aditivo de -1 e) aditivo de 1
Antonio Silvio Palmitano
el 28/10/17Plantea que las raíces de la ecuación son: x1 y x2.
Luego, observa que la ecuación tiene la forma: 1*x2 + p*x + q = 0.
Luego, recuerda las relaciones entre coeficientes y raíces:
x1 + x2 = -p,
x1*x2 = q.
Luego, tienes en tu enunciado: p = x1, q = x2,
sustituyes y tienes el sistema de ecuaciones:
x1 + x2 = -x1. aquí haces pasaje de término y queda: x2 = -2*x1 (1),
x1*x2 = x2, aquí haces pasaje de factor como divisor, y queda: x1 = 1;
luego sustituyes en la ecuación señalada (1), y queda: x2 = -2.
Luego, tienes para la suma de las raíces:
x1 + x2 = 1 + (-2) = 1 - 2 = -1, que es el inverso aditivo de 1.
Espero haberte ayudado.
-
Hola buenas!, si al realizar la A. Oblicua la n nos sale infinito, hay asintota en y=m, o no existe? Gracias!
-
Hola unicoos está bien esta derivada?
Señalen donde está el error en caso de que no sea correcta. Muchas gracias
David
el 29/10/17Esta casi perfecta. Te comiste todos los parentesis en sen(5x-2) y cos(5x-2)
No pondria √1
Y por otro lado simplificaría cos²(5x-2) / √cos(5x-2) del mismo modo que haría con 2²/√2 = 2²√2/(√2.√2)= 2²√2 / 2 = 2√2.
Por tanto escribiría cos(5x-2) . √cos(5x-2) en su lugar... O incluso √cos³(5x-2) si introducimos el factor en la raiz... Recuerda, 2√2= √(2².2)=√2³