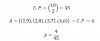-
Guillem De La Calle Vicente
el 14/4/17¿Hay un número igual de números positivos y negativos?
Para cada número positivo existe un número negativo correspondiente. ¿Implicaría eso que el número de números positivos es "igual" al número de números negativos? (¿Son incomparables porque ambos se acercan al infinito?)
Antonio
el 14/4/17Hay exactamente los mismos.
Por cada número positivo existe uno y solo uno negativo,
y por cada número negativo existe uno y solo uno positivo,
por lo que ambos conjuntos tienen el mismo cardinal.
Existe una función biyectiva del conjunto de los números positivos al conjunto de los números negativos.
-
Sandy Murillo S...
el 14/4/17HOla µnicoos, por favor os ruego que me ayudéis con un tema.
// Sean las funciones f : R→R y g : R→R tales que:
f(x) = Sen (x) y g(x) = (B+1) - B Sen (x)
Si B es un número real positivo, el valor de B para que el máximo valor posible de la función ( g - f )(x) sea 16, debe ser igual a:
a.) 6
b.) 7
c.) 8
d.) 14
e.) 15
Agradezco de antemano vuestra ayuda. Muchas gracias. Saludos.
Antonio
el 14/4/17En primer lugar debes calcular:
( g - f )(x) = [(B+1) - B Sen (x)] - Sen (x) = (B+1) - B Sen (x) - Sen (x) =
= (B+1) - [B Sen (x) + Sen (x)] = (B+1) - Sen (x) (B + 1) = (B+1) (1- Sen (x))
llegado a aquí, dos formas de seguir:
a) ( g - f )(x) = (B+1) (1- Sen (x))
como B+1 es constante y positivo: (B+1) (1- Sen (x)) se maximizará cuando lo haga 1- Sen (x).
1- Sen (x) se maximizará cuando Sen (x) se minimizará, obtenemos el máximo cuando Sen (x) se minimice, es decir en x=-π/2
Por otro lado sabemos que ( g - f )(-π/2) = 16, por lo que:
(B+1) (1- Sen (-π/2))=16
(B+1) (1- (-1))=16
B = 7
b) ( g - f )(x) = (B+1) (1- Sen (x))
Maximicemos la función:
( g - f )'(x) = (B+1) (- Cos (x))
(B+1) (- Cos (x)) = 0como B>0 => B+1≠0
Cos(x)=0 => x1=π/2 x2=-π/2
( g - f )''(x) = (B+1) Sen (x)( g - f )''(π/2) = (B+1) Sen (π/2) = (B+1)>0 => mínimo
( g - f )''(-π/2) = (B+1) Sen (-π/2) = -(B+1)<0 => máximo en x=-π/2
Por otro lado sabemos que ( g - f )(-π/2) = 16, por lo que:
(B+1) (1- Sen (-π/2))=16
(B+1) (1- (-1))=16
B = 7
-
Toby
el 14/4/17 -
Deidara Stick.
el 14/4/17 -
paola
el 14/4/17
Buenos días! ¿Podría alguien echarme una mano y ayudarme con un ejercicio de RECTAS Y PLANOS EN EL ESPACIO ?? He justificado la afirmación del enunciado y planteado el apartado a (aunque no creo que el razonamiento sea acertado) pero el b y el c se me resisten... ¿puede alguien ayudarme con los apartados a, b y c? -
Antonio Martinez Parra
el 14/4/17buenas
ejercicio de angulos ,por favor desarrollado para ver mi fallo.
gracias
Deidara Stick.
el 14/4/17Hola!!
Sabemos solo que A+C=94
Entonces A+B+C+D=180
(A+C)+(B+D)=180
84+(B+D)=180
B+D=180-94
B+D=86 _____________________ Como B=D por ser ángulos correspondientes internos ; así B=43 y D=4
de igual manera con A y C, A+C=94 ; pero A=C...... entonces A=47 y C=47
(C y E), (B y H) son ángulos alternos internos. Así (C=E) y (B=H)
(A y G), (D y F) son ángulos alternos externos. Así (A=G) y (D=F)
A=47, B=43, C=47, D=43, E=47, F=43, G=47 y H=43. Espero haberte ayudado!!.
-
vanny
el 14/4/17 -
Angelo Gallegos Parra
el 14/4/17
ayudenme porfavor es sobre induccion 
David
el 17/4/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Usuario eliminado
el 14/4/17Hola! No puedo resolver un problema textual de cálculo integral cuando tengo dos funciones distintas.¿Pueden ayudarme por favor? Gracias
-
Laura
el 14/4/17
Buenas noches, me ayudarían con este ejercicio de probabilidad. Lo hice de 2 formas pero no da igual, se que la primera es la correcta pero no entiendo porque no me da por el segundo método. En el segundo use la intersección y luego la unión. Me podríaNo decir porque no me da gracias.
