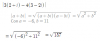-
Bet
el 5/1/17
Cómo planteo esto de forma escrita? La saqué por lógica pero necesito saber cómo se puede plantear de forma escrita :'(
Gracias de antemano
Antonio Silvio Palmitano
el 5/1/17Llamemos:
m: cantidad de mujeres en 4° A
h: cantidad de hombres en 4° A
luego tienes la relación: m = 2h,
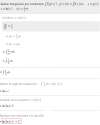
y la probabilidad de elegir un hombre en 4° A queda:
p = h/(m+h) = h(2h+h) = h / 3h = 1/3.
Luego, llamemos:
M: cantidad de mujeres en 4° B
H: cantidad de hombres en 4° B
luego tienes la relación: H = M-5,
y la probabilidad de elegir un hombre en 4° B queda:
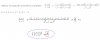
P = H/(M+H) = (M-5)/(M+M-5) = (M-5)/(2M-5).
Luego, como tienes que las probabilidades son iguales, planteamos P = p, sustituimos y queda:
(M-5)/(2M-5) = 1/3, hacemos pasajes de divisores como factores y queda:
3(M-5) = 2M-5, distribuimos el primer miembro y queda:
3M - 15 = 2M - 5, hacemos pasajes de términos, reducimos términos semejantes y queda:
M = 10, de donde tenemos: H = 10 - 5 = 5, y la cantidad total de alumnos de 4° B queda: N = 15.
Espero haberte ayudado.
-
Enrique Sánchez Sancho
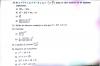
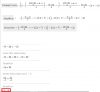
el 5/1/17Me ayudaría mucho hacer desde la 37 hasta la 40.
37 : ∫ X2 e x^3 dx 38) ∫ 1654 √(2x+1) dx 39) ∫ dx/(xlnx) 40 ) ∫ dx/ (√ (x+4 ) - √ (x+3) )
-
Carlos Ojeda
el 5/1/17 -
Alejandro soto
el 5/1/17 -
JUAN AMPIE
el 5/1/17
Una ayuda por favor de este foro por favor
-
Andres
el 5/1/17Como puedo encontrar los puntos de una función, donde la recta tangente tenga un pendiente determinada, por ejemplo 1?
Muchas gracias
-
Enrique Sánchez Sancho
el 5/1/17¿Esta integral está bien ? : ∫ x2
x^2 = ∫ x2 ∫3x2
Enrique Sánchez Sancho
el 5/1/17
Axel Morales Piñón.
el 5/1/17 -
Enrique Sánchez Sancho
el 5/1/17¿Puedo resolver esta integral por partes:? ∫1/X cos (ln (x^3)) dx = EHHH.... ¿cómo empiezo?
Enrique Sánchez Sancho
el 5/1/17 -
loredana nedelcu
el 5/1/17 -
Gerardo
el 5/1/17Hola buen día espero puedan ayudarme en este problema de algebra, me siento un poco confundido ya que lo he resolvido por gauss y he podido dar condiciones pero aun no me queda claro como finalizarlo
Encuentre valores de a,b,c tales que el sistema tenga solución, no tenga solución y tenga infinitas soluciones
x+3y+z=a
-x-2y+z=b
3x+7y-z=c
De antemano muchas gracias!!! :D
Antonio Silvio Palmitano
el 5/1/17Planteamos la matriz ampliada del sistema:
1 3 1 a
-1 -2 1 b
3 7 -1 c
A la fila 2 le sumamos la fila 1, a la fila 3 le restamos el triple de la fila 1, y queda:
1 3 1 a
0 1 2 (a+b)
0 -2 -4 (-3a+c)
A la fila 1 le restamos el triple de la fila 2, a la fila 3 le sumamos el doble de la fila 2, y queda:
1 0 -5 (-2a-3b)
0 1 2 (a+b)
0 0 0 (-a+2b+c)
Luego, observa que el rango de la matriz del sistema es 2, y que tenemos dos opciones para el rango de la matriz ampliada:
1) Si -a+2b+c=0 tenemos que el rango de la matriz ampliada es 2 y el sistema resulta ser compatible indeterminado, y con infinitas soluciones.
2) Si -a+2b+c≠0 tenemos que el rango de la matriz ampliada es 3 y el sistema resulta ser incompatible, y sin solución.
El sistema nunca puede ser compatible determinado, con única solución.
Espero haberte ayudado.
Cristopher Brian Lemke Vásquez
el 5/1/17Si planteas el sistema como una matriz y a, b, c son los términos de la matriz ampliada:
- Si el rango de la matriz es igual al rango de la matriz ampliada y éste es igual al número de incógnitas, el sistema tiene solución.
- Si el rango de la matriz es igual al rango de la matriz ampliada y éste es menor al número de incógnitas, el sistema tiene infinitas soluciones.
- Si el rango de la matriz es diferente al rango de la matriz ampliada, el sistema no tiene solución.
Si sacas el determinante de la matriz ampliada, obtendrás algo así como -5a + 10b -4a (igual me equivoco, hazlo por si acaso) y tendrás que buscar valores para a, b y c que cumplan con las condiciones anteriores.El rango de la matriz del sistema es 2 y el número de incógnitas 3, así que nunca podrá ser compatible determinado (¡pregunta trampa!)
¡Suerte!
