-
pvdk
el 27/5/18 -
Pablo Vicente
el 27/5/18 -
Ignacio Vergara
el 27/5/18 -
destru
el 27/5/18 -
Nicolás Conde Otero
el 27/5/18Hola puedes hacer algún vídeo explicando cinemática?
Quikaragon
el 27/5/18 -
Rocío NP
el 27/5/18Buenas! Tengo una duda con un problema ya que no sé cómo plantearlo.. El problema es el siguiente: Halla el coeficiente de rozamiento entre el suelo y una escalera de mano de 3 metros apoyada en la pared (no hay rozamiento con la pared) y en el suelo y formando un ángulo de 60º con la horizontal para que se mantenga en equilibrio. Gracias!
Raúl RC
el 27/5/18
Antonio Silvio Palmitano
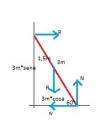
el 28/5/18
Observa el diagrama, y tienes que sobre la escalera están aplicadas cuatro fuerzas, de las que indicamos sus direcciones y sentidos en la imagen, y de las que indicamos sus módulos y brazos de momento (torque) con respecto al punto de apoyo de la escalera contra el suelo:
Peso: P = M*g, bP = 1,5*cos(60°);
Reacción normal de la pared: R, bR = 3*sen(60°);
Reacción normal del suelo: N, bN = 0;
Rozamiento del suelo: fr = μ*N, bfr = 0.
Luego, aplicas la Primera Ley de Newton (observa que agregamos la ecuación de equilibrio rotacional, en la que indicamos a los momentos (torques) con M), y queda el sistema de tres ecuaciones:
R + fr = 0,
N + P = 0,
MR + Mfr + MN + MP = 0.
Luego, sustituyes expresiones (observa que consideramos un sistema de coordenadas OXY usual, con sentido de rotación antihorario con signo positivo):
R - μ*N = 0, aquí sumas μ*N en ambos miembros, y queda: R = μ*N (1),
N - M*g = 0, aquí sumas M*g en ambos miembros, y qued: N = M*g (2),
-R*3*sen(60°) + μ*N*0 + N*0 + M*g*1,5*cos(60°) = 0;
luego, cancelas términos nulos en la tercera ecuación, sustituyes en ella las expresiones señaladas (1) (2), y queda:
-μ*M*g*3*sen(60°) + M*g*1,5*cos(60°) = 0,
divides por -1,5*M*g en todos los términos de la ecuación, y queda:
μ*2*sen(60°) - cos(60°) = 0,
sumas cos(60°) en ambos miembros, y queda:
μ*2*sen(60°) = cos(60°),
divides por 2*sen(60°) en ambos miembros, y queda:
μ = cos(60°) / 2*sen(60°),
divides por cos(60°) en el numerador y en el denominador del segundo miembro, y queda:
μ = 1 / ( 2*tan(60°) ) = 1 / ( 2*√(3) ) ≅ 0,2887.
Espero haberte ayudado.
-
Steph
el 27/5/18
Alguien me puede ayudar con este ejercicio porfa?
Steph
el 27/5/18El circuito de la figura esta formado por resistencias: R1, R2, R3, de valores respectivos 6, 8 y 4 ohmios. La ddp Vcd= 14 V. Determina
a) La ddp Vcd.
b) La intensidad que pasa por cada resistencia y la intensidad total.
c) La ddp de cada resistencia.
d) La resistencia equivalente del circuito
-
diegotesbo
el 27/5/18 -
Carlos
el 27/5/18
Hola, quería hacer una pregunta, en hidrostatica, recuerdo que vimos ejercicios en los que actuaban las diferentes dimensiones de un cuerpo, como se calculan este tipo de ejercicios?
-
Marta Pérez Paredes
el 27/5/18Hola tengo una duda en un apartado de un ejercicio en cuestión.
Un cuerpo de 5 kg asciende 18 m por un plano inclinado 60º al aplicarle una fuerza de 75N paralela al plano.Suponiendo un coeficiente de rozamiento de 0'14.
Determina el incremento de energía potencial.
DAVID CAMILO GOMEZ MEDINA
el 27/5/18Hola, yo lo asociaría con el trabajo de una fuerza no conservativa. Trabajo de una fuerza conservativa es igual al delta de la energía mecánica, o mejor, el delta de la energía cinética más el delta de la energía potencial. Ahí saldría. Me avisas si no fui claro con la explicación.
